Quick Overview
- $$\displaystyle \frac d {dx}\left(f(x)\cdot g(x)\right) = f'(x)g(x) + f(x)g'(x)$$
- The examples and questions in this lesson assume you know the Basic Derivatives from earlier lessons.
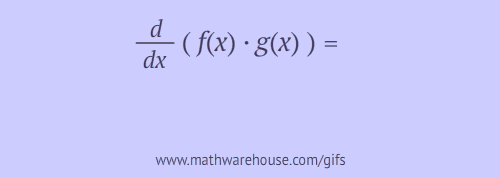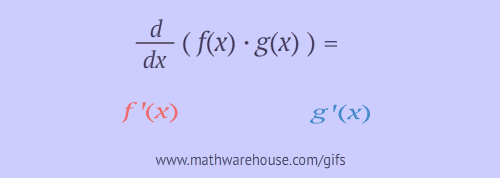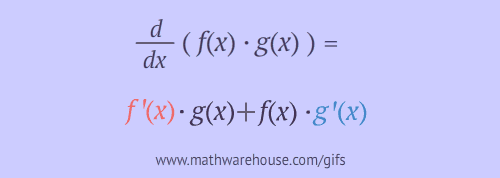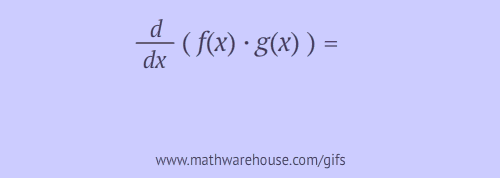
Explanation
When differentiating a product, each factor is differentiated, but one at a time. You can think of this as "each factor gets a turn at being the derivative."
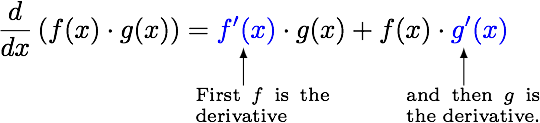
This pattern holds true, even when there are more than two factors in the product, as shown below.
$$ \frac d {dx}\left(f(x)\cdot g(x) \cdot h(x)\right) = \blue{f'(x)}\cdot g(x)\cdot h(x) + f(x)\cdot \blue{g'(x)}\cdot h(x) + f(x)\cdot g(x)\cdot\blue{h'(x)} $$
Examples
Example 1---Two Factors
Suppose $$f(x) = x^2\sin 3x$$. Find $$f'(x)$$.
Step 1Identify the factors in the function.
$$ f(x) = \blue{x^2}\cdot \red{\sin 3x} $$
Step 2Use the product rule to differentiate the function.
$$ f'(x) = \blue{2x}\sin 3x + x^2\red{(3\cos 3x)} = 2x\sin 3x + 3x^2\cos 3x $$
Answer$$f'(x) = 2x\sin 3x + 3x^2\cos 3x$$
Example 2---Three Factors
Suppose $$f(x) = 4x^3\,e^{-2x}\cos 6x$$. Find $$f'(x)$$
Step 1Identify the factors that make up the function.
$$ f(x) = 4x^3\blue{e^{-2x}}\red{\cos 6x} $$
Step 2Differentiate using the product rule. The parts in $$\blue{blue}$$ are the derivatives of the individual factors.
$$ \begin{align*}% f'(x) & = \big[\blue{12x^2}\,e^{-2x}\cos 6x\big] + \big[4x^3\blue{(-2e^{-2x})}\cos 6x\big] + \big[4x^3\,e^{-2x}\blue{(-6\sin 6x)}\big]\\[6pt] & = 12x^2\,e^{-2x}\cos 6x - 8x^3e^{-2x}\cos 6x - 24x^3\,e^{-2x}\sin 6x \end{align*} $$
Step 3(Optional) Write the derivative in a factored form.
$$ \begin{align*} f'(x) & = 12x^2\,\blue{e^{-2x}}\cos 6x - 8x^3\blue{e^{-2x}}\cos 6x - 24x^3\,\blue{e^{-2x}}\sin 6x\\[6pt] & = \blue{e^{-2x}}\left(12\red{x^2}\cos 6x - 8\red{x^3}\cos 6x - 24\red{x^3}\sin 6x\right)\\[6pt] & = \red{x^2}e^{-2x}\left(12\cos 6x - 8x\cos 6x - 24x\sin 6x\right)\\[6pt] & = 4x^2e^{-2x}\left(3\cos 6x - 2x\cos 6x - 6x\sin 6x\right) \end{align*} $$
Answer$$f'(x) = 4x^2e^{-2x}\left(3\cos 6x - 2x\cos 6x - 6x\sin 6x\right)$$.


















