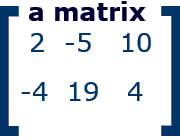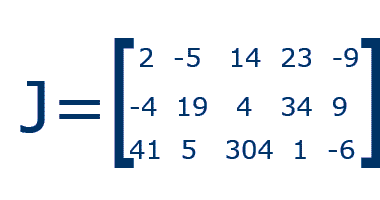A matrix is a way to organize data in columns and rows. A matrix is written inside brackets [ ]. Look at the picture below to see an example.
Each item in a matrix is called an entry.
Dimension of Matrix
The dimensions of a matrix refer to the number of rows and columns of a given matrix. By convention the dimension of a a matrix are given by number of rows • number of columns.
One way that some people remember that the notation for matrix dimensions is rows by columns (Rather than columns by rows) is by recalling a once popular-soda:
RC Cola -- rows before columns!
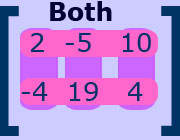
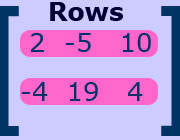
Below, you can see two pictures of the same matrix with the rows and columns highlighted.
The dimensions of this matrix:- dimensions: 2 × 3
- 2 rows × 3 columns

Matrix Notation
In order to identify an entry in a matrix, we simply write a subscript of the respective entry's row followed by the column.

In matrix A on the left, we write a23 to denote the entry in the second row and the third column.
One way to remember that this notation puts rows first and columns second is to think of it like reading a book. You always read sideways first, just as you always write the rows first. To continue the analogy, when you are done reading a row in a book, your eyes move downward, just as the columns after the rows. A23 indicates the row number first, 2, then the column number 3.
Practice Identifying Entries
Practice 1
What are the dimensions of the matrix below?
The dimensions of the matrix are 3 × 3 (3 rows × 3 columns).
What are the dimensions of J?
The dimensions are 3 × 5 (3 rows × 5 columns).
Practice 2
Practice 3
What are the dimensions of V below?
The dimensions of the matrix are 4 × 5 (4 rows × 5 columns).
Identify entry v14
The entry is 31, (row 1 & column 4).
What is the matrix notation to denote the entry in the bottom right corner, 15?
v45 denotes the entry in the fourth row and fifth column, the number 15 in the bottom right corner.
Adding and Subtracting Matrices
To add or subtract matrices, you just add or subtract the corresponding entries (the entries or numbers that are in the same spot).

Why are the same dimensions required for addition and subtraction?
Think about it: Since adding/subtracting matrices involves adding/subtracting corresponding entries. What would you do with the entries in the one matrix that do not have a corresponding entry in the other?)
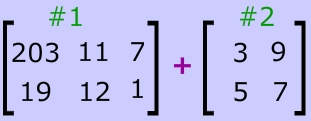
Consider the example pictured up above. Matrix #1 has one more column than Matrix #2. How would you match, let alone add, the entries of #1's column 3 with corresponding ones in #2. Well, the answer is - you can't since you cannot add matrixes unless they have the same number of rows and columns.