Matrix Equalities & Variables

Matrices can be equal if certain conditions are satisfied. Therefore, we can set up equations and solve for variables with two equal matrices. (Note: this is different from a Matrix Equationin which an entire matrix acts as a variable.)

This Page: Variables & Matrices
Other Pages: Introduction to Matrices | Matrix Equations | Real World Matrices

Equal of Matrices

Two matrices are equal if and only if these matrices have the same dimensions and equal corresponding elements.

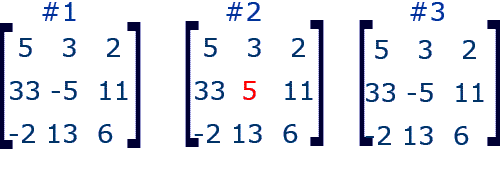
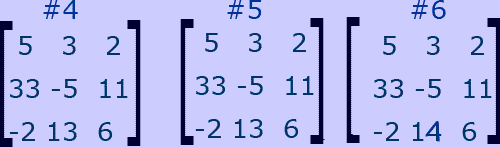
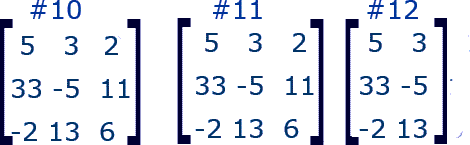
Which matrices below are equal?

All three matrices have the same dimensions
- 3 × 3 (3 rows and 3 columns)
All corresponding entries or elements are the same in matrix 1 and matrix 3.
- The middlemost entry of matrix #2 is not the same as the corresponding entry in the other matrices. Therefore, matrix #2 does not equal either of the other ones.

Which matrices below are equal? Answer

Which matrices below are equal? Answer

Which matrices below are equal?
Answer

Solving for Variables in Matrices

If we know that two matrices are equal, we can find the value of variables in matrices. Since equal matrices have equal corresponding entries, we can set an unknown entry in one matrix equal to its corresponding partner in the other matrix.

To find the value of the variable y in the left hand matrix, we just set it equal to its corresponding entry in the right hand matrix.
y = 33

Solving for variables in equal matrices will not always be as easy as matching a variable with a corresponding number. Here's a slightly more challenging problem: What is the value of y?

Answer

This Page: Variables & Matrices
Other Pages: Introduction to Matrices | Matrix Equations | Real World Matrices