Example One
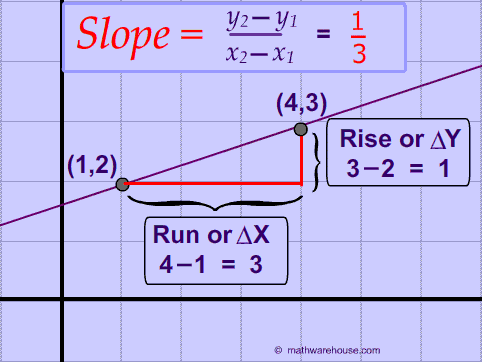
The slope of a line going through the point (1, 2) and the point (4, 3) is $$ \frac{1}{3}$$.
Remember: difference in the y values goes in the numerator of formula, and the difference in the x values goes in denominator of the formula.
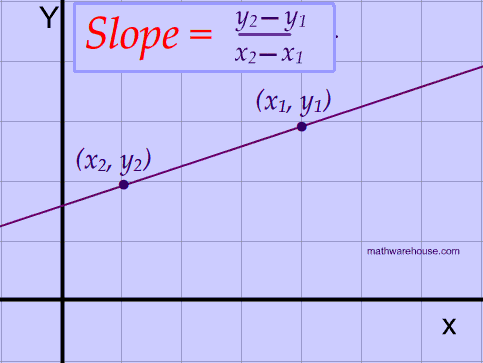
The slope of a line characterizes the direction of a line. To find the slope, you divide the difference of the y-coordinates of 2 points on a line by the difference of the x-coordinates of those same 2 points.
Different words, same formula
Teachers use different words for the y-coordinates and the the x-coordinates.
- Some call the y-coordinates the rise and the x-coordinates the run.
- Others prefer to use $$ \Delta $$ notation and call the y-coordinates $$ \Delta y$$ , and the x-coordinates the $$ \Delta x$$ .
These words all mean the same thing, which is that the y values are on the top of the formula (numerator) and the x values are on the bottom of the formula (denominator)!
Can either point be $$( x_1 , y_1 ) $$ ?
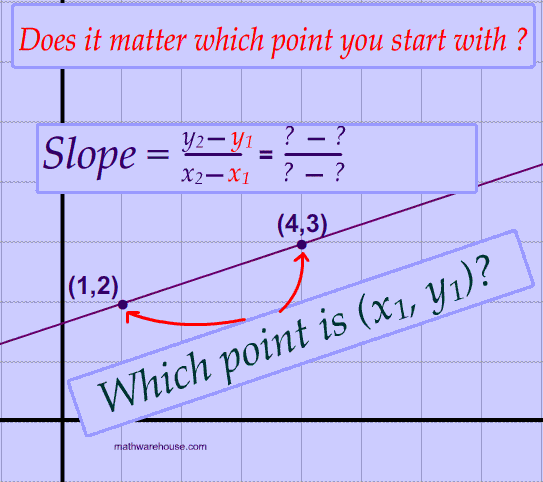
There is only one way to know!
First, we will use point (1, 2) as $$x_1, y_1$$, and as you can see : the slope is: $ \boxed {\frac{1}{3} }$ .
Now let's use point (4, 3) as $$x_1, y_1$$, and as you can see , the slope simplifies to the same value: $ \boxed {\frac{1}{3} }$ .
The work , side by side
point (4, 3) as $$ (x_1, y_1 )$$
$$ slope = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{3-2}{4-1} = \frac{1}{3} $$
point (1, 2) as $$ (x_1, y_1 )$$
$$ slope = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{2-3}{1-4} = \frac{-1}{-3} = \frac{1}{3} $$
Answer: It does not matter which point you put first. You can start with (4, 3) or with (1, 2) and, either way, you end with the exact same number! $$ \frac{1}{3} $$
Example 2 of the Slope of A line
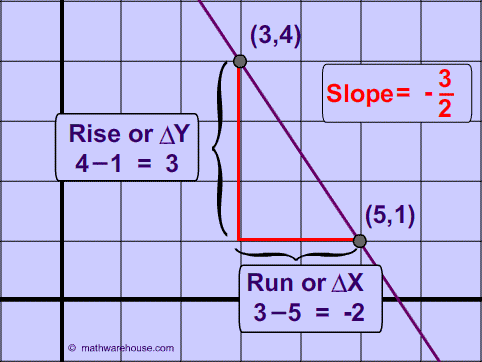
The slope of a line through the points (3, 4) and (5, 1) is $$- \frac{3}{2}$$ because every time that the line goes down by 3(the change in y or the rise) the line moves to the right (the run) by 2.
Video Tutorial on the Slope of a Line
Slope of vertical and horizontal lines
The slope of a vertical line is undefined
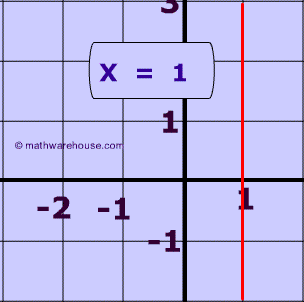
This is because any vertical line has a $$\Delta x$$ or "run" of zero. Whenever zero is the denominator of the fraction in this case of the fraction representing the slope of a line, the fraction is undefined. The picture below shows a vertical line (x = 1).
The slope of a horizontal line is zero
This is because any horizontal line has a $$\Delta y$$ or "rise" of zero. Therefore, regardless of what the run is (provided its' not also zero!), the fraction representing slope has a zero in its numerator. Therefore, the slope must evaluate to zero. Below is a picture of a horizontal line -- you can see that it does not have any 'rise' to it.
Do any two points on a line have the same slope?
Answer: Yes, and this is a fundamental point to remember about calculating slope.
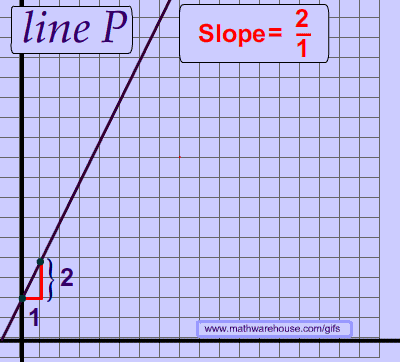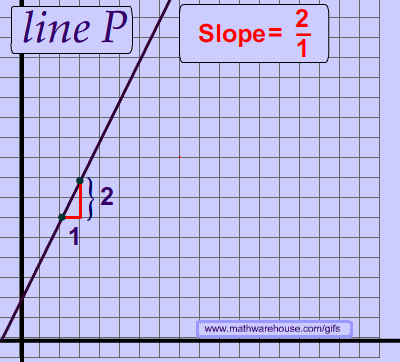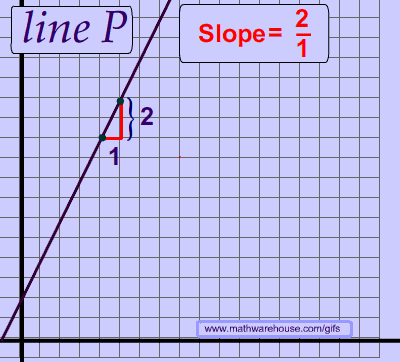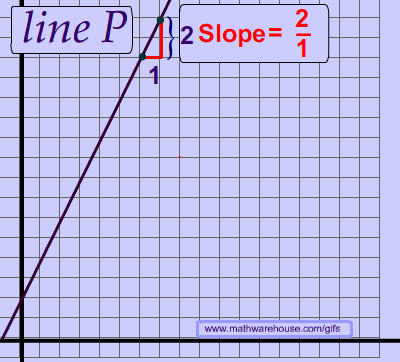
Every line has a consistent slope. In other words, the slope of a line never changes. This fundamental idea means that you can choose any 2 points on a line.
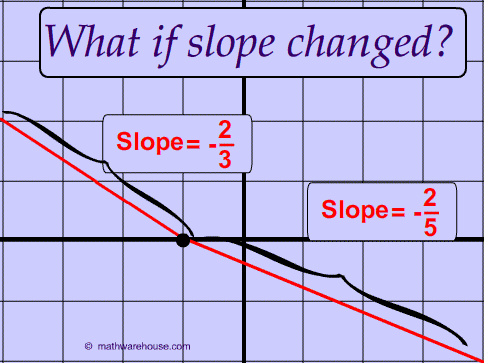
Think about the idea of a straight line. If the slope of a line changed, then it would be a zigzag line and not a straight line, as you can see in the picture above.
As you can see below, the slope is the same no matter which 2 points you chose.
The Slope of a Line Never Changes
Practice Problems
Problem 1
$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}
$
Using $$ \red{ (10,3)}$$ as $$x_1, y_1$$
$ \frac{9- \red 3}{7- \red{10}} \\ = \frac{6}{-3} \\ = \boxed {-2 } $
Using $$ \red{ (7,9)} $$ as $$x_1, y_1$$
$ \frac{3- \red 9}{10- \red 7} \\ =\frac{-6}{3} \\ = \boxed{-2 } $
Problem 2
$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}
$
Using $$ \red{ ( 4,3 )}$$ as $$x_1, y_1$$
$ = \frac{-2 - \red 3}{4- \red 4} \\ = \frac{-5}{ \color{red}{0}} \\ = \text{undefined} $
Using $$ \red{ ( 4, -2 )}$$ as $$x_1, y_1$$
$ = \frac{3- \red{-2}}{4- \red 4} \\ = \frac{5}{ \color{red}{0}} \\ = \text{undefined} $
Whenever the run of a line is zero, the slope is undefined. This is because there is a zero in the denominator of the slope! Any the slope of any vertical line is undefined .
Problem 3
$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}
$
Using $$ \red{ ( 8, 7 )}$$ as $$x_1, y_1$$
$ \frac{10 - \red 7}{2 - \red 8} \\ = \frac{3}{-6} \\ = -\frac{1}{2} $
Using $$ \red{ ( 2,10 )}$$ as $$x_1, y_1$$
$ \frac{7 - \red {10}}{8- \red 2} \\ = \frac{-3}{6} \\ = -\frac{1}{2} $
Problem 4
$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}
$
Using $$ \red{ (7,3 )}$$ as $$x_1, y_1$$
$$ \frac{ 5- \red 3}{8- \red 7} \\ = \frac{2}{1} \\ = 2 $$
Using $$ \red{ ( 8,5 )}$$ as $$x_1, y_1$$
$$ \frac{ 3- \red 5}{7- \red 8} \\= \frac{-2}{-1} \\ = 2 $$
Problem 5
$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}
$
Using $$ \red{ ( 5, 9)}$$ as $$x_1, y_1$$
$$ \frac{ 11 - \red 5}{12- \red 9} \\ = \frac{6}{3} \\ =2 $$
Using $$ \red{ (12, 11 )}$$ as $$x_1, y_1$$
$$ \frac{ 5- \red{ 11} }{9- \red { 12}} \\ = \frac{-6}{-3} \\ = 2 $$
Problem 6
$
\frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}
$
Using $$ \red{ ( 4,5 )}$$ as $$x_1, y_1$$
$$ \frac{ 2 - \red 5}{4- \red 4} \\ = \frac{ -3}{\color{red}{0}} \\ = undefined $$
Using $$ \red{ ( 4,2 )}$$ as $$x_1, y_1$$
$$ \frac{ 5 - \red 2}{4- \red 4} \\ = \frac{ 3}{\color{red}{0}} \\ = undefined $$
WARNING! Can you catch the error in the following problem Jennifer was trying to find the slope that goes through the points $$(\color{blue}{1},\color{red}{3})$$ and $$ (\color{blue}{2}, \color{red}{6})$$ . She was having a bit of trouble applying the slope formula, tried to calculate slope 3 times, and she came up with 3 different answers. Can you determine the correct answer?
Challenge Problem
Slope Practice Problem Generator
You can practice solving this sort of problem as much as you would like with the slope problem generator below.
It will randomly generate numbers and ask for the slope of the line through those two points. You can chose how large the numbers will be by adjusting the difficulty level.
Related pages:
