How to express a vector as an ordered pair
Follow these steps:
Align the 'tail' of the vector with the origin.
Determine the x and y coordinates where the head or 'pointy end' of the vector lands. Typically, for this you need to use sine and cosine ratios .
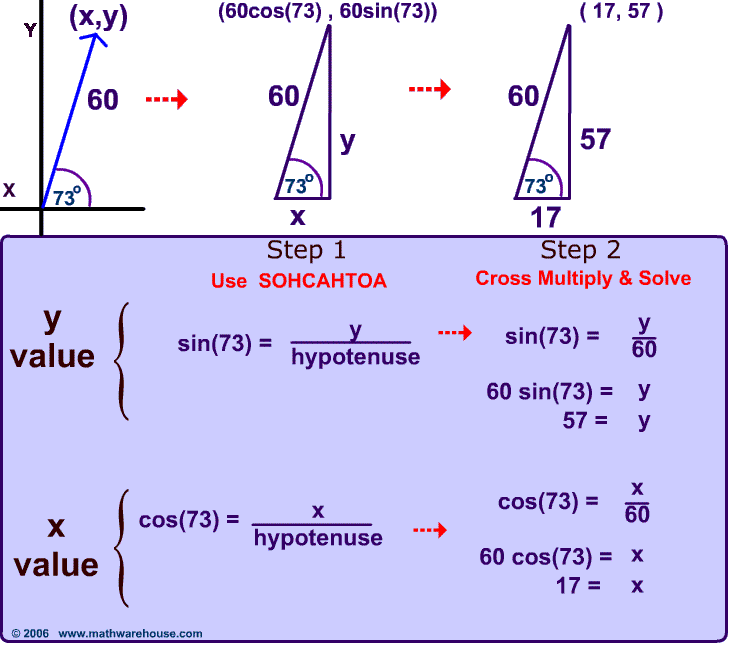
In the picture below, the vector has a magnitude of 60 and its direction is 73° above the positive x axis.
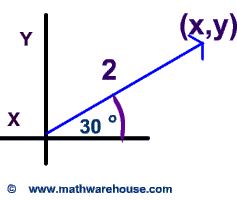
Problem 1
Show Answer
Express the vector's coordinates below as ordered pairs in simplest radical form.
$$
\text{X Coordinate}
\\
= 2 \cdot { \bf cos}(30^{\circ})
\\
= 2 \cdot \frac{\sqrt{3}}{2}= \red{ \sqrt{3}}
$$
$$
\text{Y Coordinate}
\\
= 2 \cdot { \bf sin}(30^{\circ})
\\
= 2 \cdot \frac{1}{2}= \red 2
$$
$$ (\sqrt{3}, 2) $$
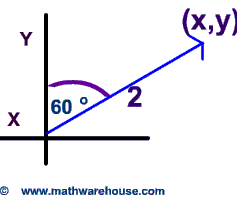
Problem 2
Show Answer
Express the vectors coordinates below as ordered pairs in simplest radical form.
This was kind of a trick question in that you must recognize that the 60° angle is the same as the prior problem's angle( i.e. it is 30° from the x-axis ).
$$
\text{X Coordinate}
\\
= 2 \cdot { \bf sin}(60^{\circ})
\\
= 2 \cdot \frac{\sqrt{3}}{2}= \red{ \sqrt{3}}
$$
$$
\text{Y Coordinate}
\\
= 2 \cdot { \bf sin}(30^{\circ})
\\
= 2 \cdot \frac{1}{2}= \red 2
$$
$$ (\sqrt{3}, 2) $$
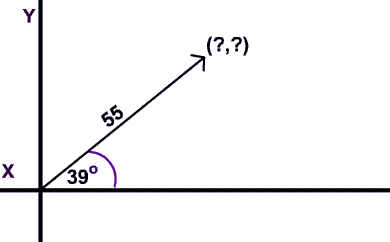
Problem 3
Problem 4