How Period of Sine and Cosine graphs relates to their equation and to unit circle. Interactive demonstration of period of graphs

What is the period of a sine cosine curve?

The Period is how long it takes for the curve to repeat.

As the picture below shows, you can 'start' the period anywhere, you just have to start somewhere on the curve and 'end' the next time that you see the curve at that height.

diagram of graph of period for sin of half theta

So, what is the formula for the period?

If you look at the prior 3 pictures, you might notice a pattern emerge.. The period has a relationship to the value before the $$ \theta $$.

This pattern is probably easiest to see if we make a table.

Equation	Period	Picture
$$ y = sin ( \color{red}{1}\theta )$$	$$ \color{red}{2} \pi $$
$$ y = sin ( \color{red}{2}\theta )$$	$$ \color{red}{ 1 }\pi $$
$$ y = sin ( \color{red}{\frac{1}{2}}\theta )$$	$$ \color{red}{ 4\pi } $$
$$ y = sin ( \color{red}{4}\theta )$$	$$ \color{red}{ \frac{1}{2} \pi } $$

Can you guess the general formula?

As you might have noticed there is a relationship between the coefficient in front of $$ \theta$$ and the period. In the general formula, this coefficient is typically labelled as 'a'.

The general formula for $$ sin( \color{red}{a} \theta )$$ or $$ cos( \color{red}{a} \theta )$$ is.

$ period = \frac{2 \pi}{ \color{red}{a}} $

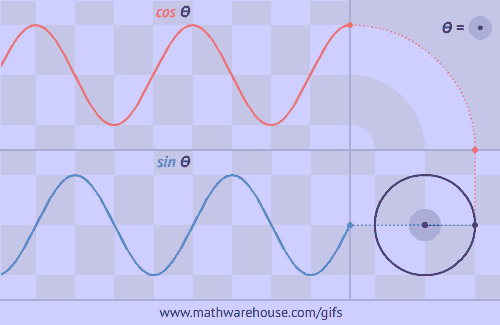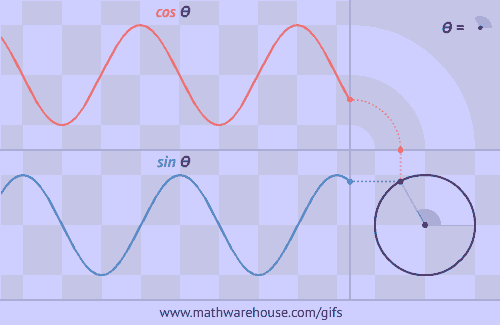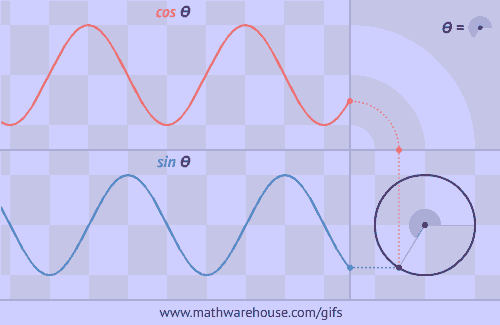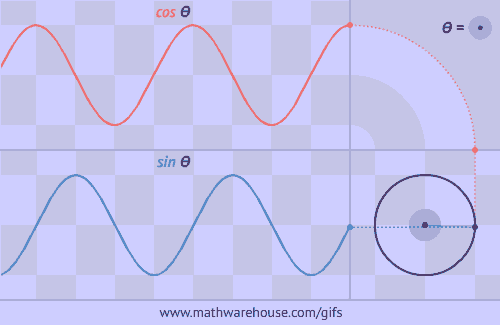
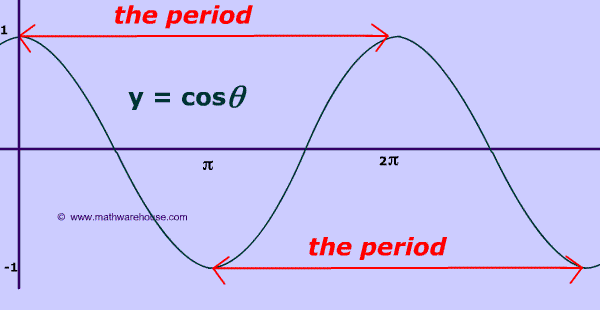
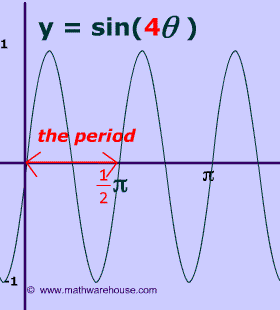
Practice Problems

Problem 1

Based on the graph below, what is the period?

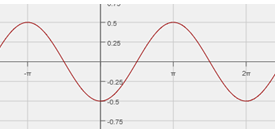
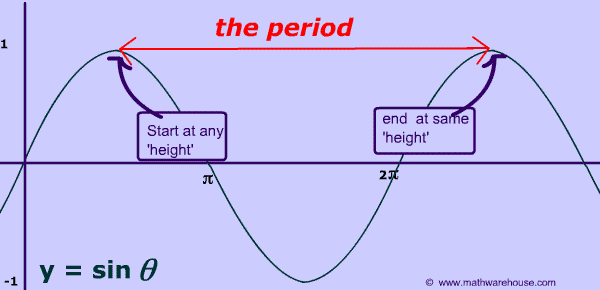
To solve these problems, just start at the x-axis and look for the first time that the graph returns to that 'height.' So, in this case, we're looking for the time when the graph returns to the -.5 value which is at $$ 2 \pi$$.

Problem 2

Based on the graph below, what is the period?

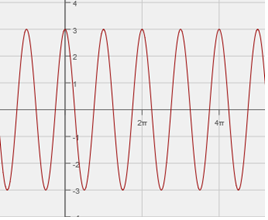
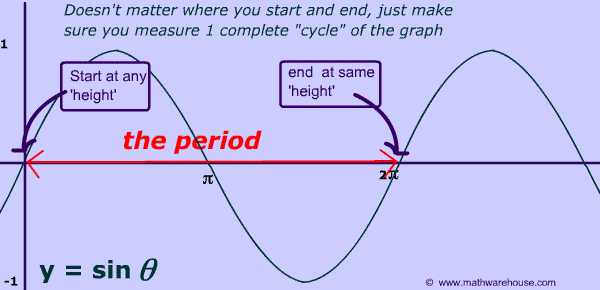
Remember: Find the height of the graph at the x-axis and then look for the first time that the graph returns to that height. In this case, the answer is $$ \pi $$ or just $$ \pi $$.

Problem 3

What is the period of the equation $$ y = -2sin(x) $$?

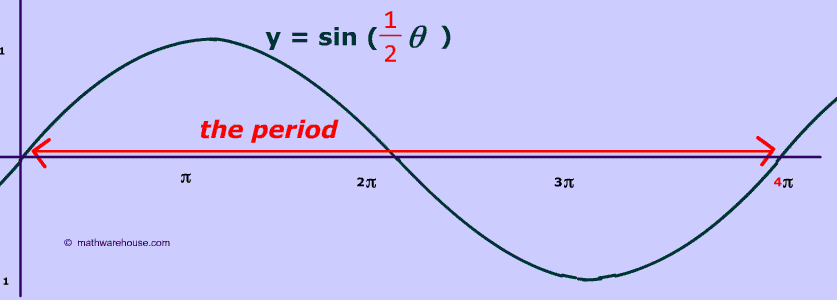
Remember: The formula for the period only cares about the coefficient, $$ \color{red}{a} $$ in front of the x. The formula for the period is the coefficient is 1 as you can see by the 'hidden' 1:

$ -2sin( \color{red}{1}x) $

$ period = \frac{2 \pi}{ \color{red}{a}} \\ period = \frac{2 \pi}{1} \\ period = 2 \pi $

Problem 4

What is the period of the equation $$ y = -7cos(8x) $$?

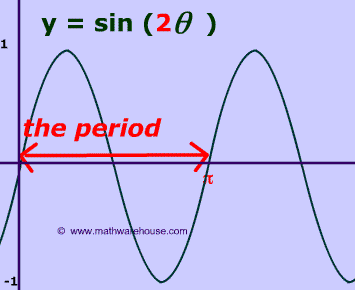
Remember: The formula for the period only cares about the coefficient, $$ \color{red}{a} $$ in front of the x. The formula for the period is the coefficient is 8:

$ -7 cos ( \color{red}{8}x) $

$ period = \frac{2 \pi}{ \color{red}{a}} \\ period = \frac{2 \pi}{ 8} \\ period = \frac{ \pi}{4} $

Problem 5

What is the period of the equation $$ y = 3cos(-2x) $$?

So, the big question here is: what do we do about the negative sign? Well, the answer is, we do not worry about the negative sign. Period tells us how long something is, and it must be a positive number.

$ 3cos( -\color{red}{2}x) $

$ period = \frac{2 \pi}{ \color{red}{a}} \\ period = \frac{2 \pi}{2} \\ period = \pi $