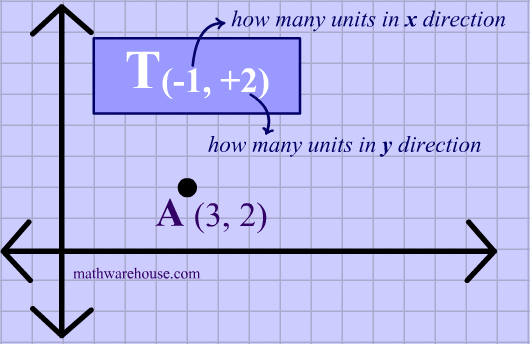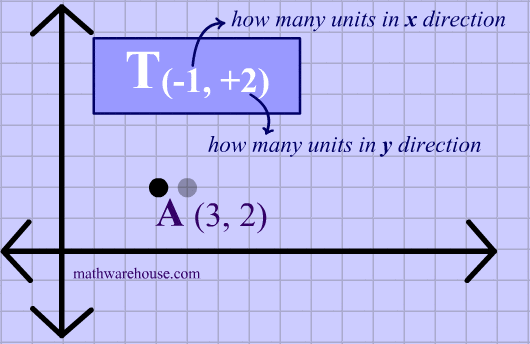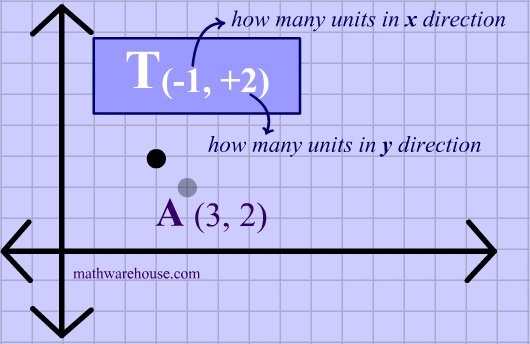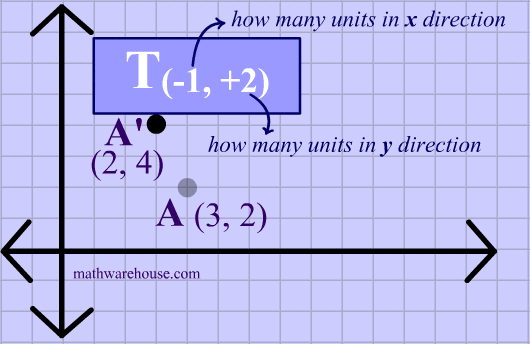Example 1
It's all about sliding
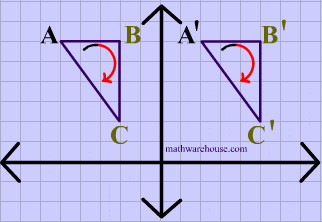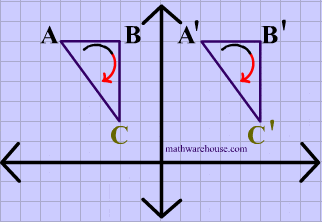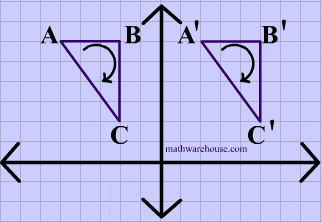
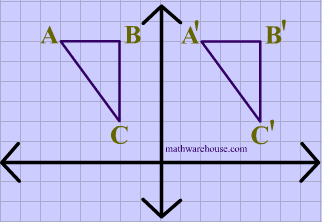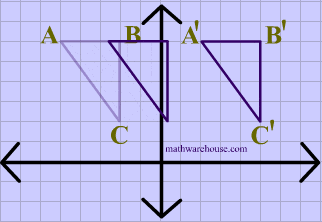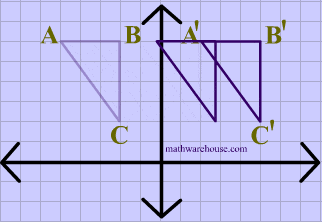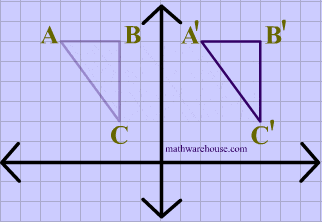
The animation below shows a triangle being translated.

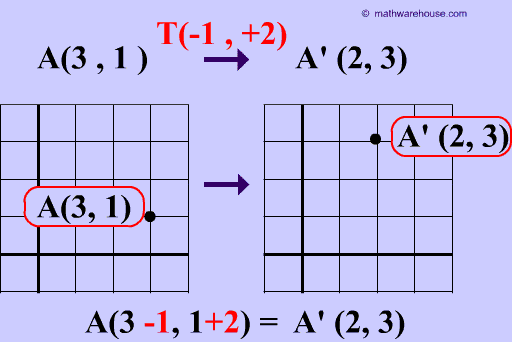
Translations are isometries . As you can see in diagram 2 below, $$ \triangle ABC $$ is translated to form its image $$ \triangle A'B'C' $$. And the distance between each of the points on the preimage is maintained in its image
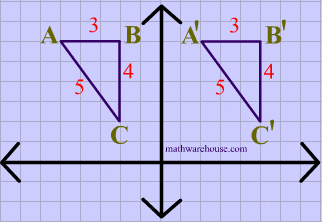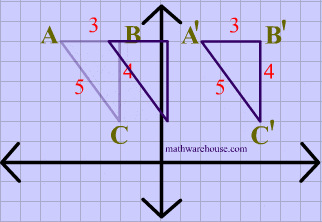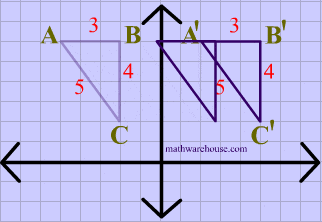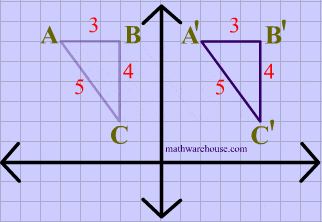
You can also see that the orientation of the letters is preserved, i.e. that the vertices in the original shape are ordered $$ABC$$ , in clockwise order, and that the image maintains the same clockwise order, making translations a direct isometry.
In translation notation, the first number represents how many units in the x direction, the second number, how many in the y direction. Both numbers tell us about how far and in what direction we are going to slide the point.
In the animation below, you can see how we actually translate the point by $$-1 $$ in the x direction and then by $$ +2$$ in the y direction .
As the animation shows a translation of $$T_{(\red{-1,+2})} $$ on the point A with coordinates $$(3,2) $$ produces an image at $$ (2,4) $$.
And $$ (3 \red{-1}, 2 \red{+2}) \rightarrow (2,4) $$.
More like Example 1...
What is the image of point B , $$ (1,5) $$ under translation of $$ T_{(-3,+2)} $$ ?
$ (1, 5) \text{ under } T_{(\red{-3}, \red{+2})} \\ (1 \red{-3}, 5 \red{+2}) \\ \boxed{(-2, 7)} $
What is the image of point B , $$ (-4,3) $$ under translation of $$ T_{(-7,-3 )} $$ ?
$ (-4, 3 ) \text{ under } T_{(\red{-7}, \red{-3 })} \\ (-4 \red{-7}, 3 \red{-3}) \\ \boxed{(-11, 0 )} $
What is the image of point B , $$ (-2a, 4b) $$ under translation of $$ T_{(+3a, +5b )} $$ ?
$ (-2a, 4b ) \text{ under } T_{(\red{+3a }, \red{ +5b })} \\ (-2a \red{+3a}, 4b \red{+5b}) \\ \boxed{(a, 9b )} $