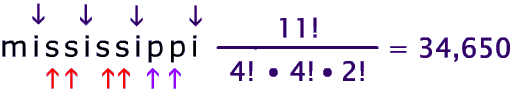How many ways can you arrange 3 letters with 1 repeat?
Compare the permutations of the letters A,B,C with those of the same number of letters, 3, but with one repeated letter $$ \rightarrow $$ A, A, B
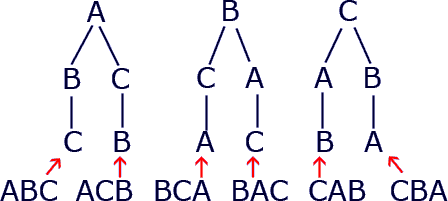
All the different arrangements of the letters A, B, C
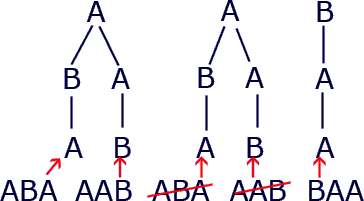
All the different arrangements of the letters A, A, B
$$ \frac{ 3!}{2!} = \frac{(3 \cdot 2 \cdot 1)}{(2 \cdot 1)} = 3 $$
If A out of N items are identical, then the number of different permutations of the N items is $$ \frac{ N! }{ A! } $$
If a set of N items contains A identical items, B identical items, and C identical items etc.., then the total number of different permutations of N objects is $ \frac{ N! }{ A! \cdot B! \cdot C! ... ! } $
Permutation Practice Problems
There is only one letter that repeats.
Since the letter o appears twice we need to divide by 2!
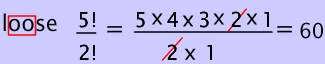
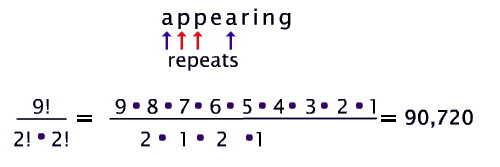
The letters a and p are the ones that repeat.
Since the letter a occurs twice and the letter p also occurs twice, we have to divide by 2! two times.
The repeats: there are four occurrences of the letter i, four occurrences of the letter s , and two occurrences of the letter p
The total number of letters is 11.