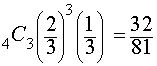$$
\text{General Formula :}
$$
$ _{\blue{ \text{total trials}}} C _{\red n} \cdot p( \text{success} ) ^{\red n} \cdot p (fail)^{\blue {total} - \red n } \\ $
Formula Summarized
I suggest you read through the explanation and lesson below to better understand the formula, but if you just want the formula and quick example for probability of an outcome occurring exactly $$\red n \text{ times}$$ over a certain number of independent events or $$\blue { trials }$$ , here you go:
$$
\text{General Formula :}
$$
$ _{\blue{ \text{total trials}}} C _{\red n} \cdot p( \text{success} ) ^{\red n} \cdot p (fail)^{\blue {total} - \red n } \\ $
Example 1
If you have a single 6 sided die , and you are going to roll the die $$\blue 8$$ times. What is the probability that you will get a 1 exactly $$ \red 2$$ times?
$ _{\blue{ \text{total trials}}} C _{\red n} \cdot p( \text{success} ) ^{\red n} \cdot p (fail)^{\blue {total} - \red n } $
$ _{\blue{ \text{8}}} C _{\red 2} \cdot \left( \frac{ 1 }{ 6 } \right) ^{\red 2} \cdot \left( \frac{ 5 }{ 6 } \right)^{\blue 8 - \red 2} \\ 28 \cdot \left( \frac{ 1 }{ 6 } \right) ^ 2 \cdot \left( \frac{ 5 }{ 6 } \right)^{6} \\ 28 \cdot \left( \frac{ 1 }{ 36 } \right) \cdot \left( \frac{ 15,625}{ 46,656 } \right) \\ \frac{ 437,500 }{ 1,679,616 } $
Second Quick Example ...
If we spin 7 times, what is the probability we will get an even number exactly $$ \red 2$$ times?
$ _{\blue{ \text{total trials}}} C _{\red n} \cdot p( \text{success} ) ^{\red n} \cdot p (fail)^{\blue {total} - \red n } \\ $
$ _{\blue 7} C _{\red 2} \cdot \left( \frac{1}{3} \right)^{\red 2} \cdot \left( \frac{2}{3} \right)^{(\blue 7 - \red 2)} \\ _7 C _2 \cdot \left( \frac{1}{3} \right)^2 \cdot \left( \frac{2}{3} \right)^{5} $
In the next part, we will explain the concepts behind this formula. If you'd like to just practice applying the formula, just go to our practice problems at the bottom of this page.
Part I. How we get the formula for multiple trial Probability
The formula to calculate the probability that an event will occur exactly n times over multiple trials is intricately tied to the formula for combinations. This may be a surprise at first, but upon examination there is a clear connection between combinations and multiple trial probabilities.
So, if you flip a coin, you have a $$\frac 1 2 $$ probability of getting heads.
What if we flip the coin twice?
What is the probablilty that we get heads twice?
This is an independent event because the first event, the coin toss, does not effect the second event, the second toss.
The probability of these two independent events is $$ \frac 1 4 $$ !
The sample space for these tosses illustrate the 4 distinct ways that the first toss followed by the second toss can play out.
| First Toss | Second Toss |
|---|---|
|
|
What if we flip the coin three times?
3 independent events
What is the probability that we will get heads exactly three times if we toss the coin three times?
The probability of getting heads all three times is $$ \frac 1 8 $$ .
Let's look at the sample space for these tosses:
| Three ways that we can get 1 Heads out of 3 tosses | ||
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
| Three ways that we can get 2 heads out of 3 tosses | ||
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 way to get 3 heads over 3 tosses | ||
|---|---|---|
|
|
|
|
|
|
|
|
Developing the Formula
If we spin the red arrow 4 times. What is the probability that we will spin an odd number on the 1st spin and even numbers on the final 3 spins?
| p(odd) | p(even) | p(even) | p(even) |
|
|
|
|
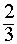
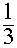
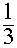
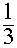
To calculate the probability of independent events simply multiply each probability together.
×
×
×
=
×
=
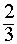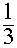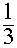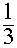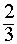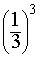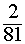
Extending the formula
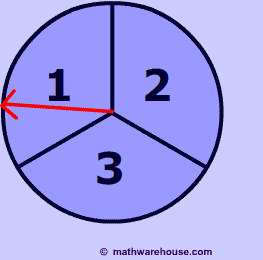
Imagine that we are using the same spinner depicted up above. Calculate the probability of obtaining exactly 1 odd number on 4 spins of the arrow. This question is different because you can get an odd number any time. Maybe on the second spin .
| 1st spin | 2nd spin | 3rd spin | 4th spin | Probability |
|---|---|---|---|---|
| p(odd) $\frac 2 3 $ | p(even) $\frac 1 3 $ | p(even) $\frac 1 3 $ | p(even) $\frac 1 3 $ |
|
| p(even) $\frac 1 3 $ | p(odd) $\frac 2 3 $ | p(even) $\frac 1 3 $ | p(even) $\frac 1 3 $ |
|
| p(even) $\frac 1 3 $ | p(even) $\frac 1 3 $ | p(odd) $\frac 2 3 $ | p(even) $\frac 1 3 $ |
|
| p(even) $\frac 1 3 $ | p(even) $\frac 1 3 $ | p(even) $\frac 1 3 $ | p(odd) $\frac 2 3 $ |
|
So, remember we changed the question. We can have an odd number for any spin, maybe there's an odd number in the first spin or in the second spin. So we add each of the $$ \frac{2}{81}$$ probabilities up to get our answer:
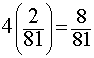Note, this is the same as
.
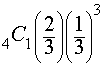So if there are 4 possible outcomes and you want exactly 1 of them to occur, the formula is $ _4 C _1 \cdot p(\text{ success})^1 \cdot p(\text{fail})^{(4-1)} \\ _4 C _1 \cdot p(\text{ success})^1 \cdot p(\text{fail})^3 $
Quick refresher on the formula for combinations in math.
Formula for Probability of Independent Events
Formula = The general formula is to determine how many combinations of the independent events can occur, then multiply the probability of each by the result of the combination. It's much easier to understand by looking at some more examples.
Problem 1
Use the formula for the probability of independent events.
$ _{\text{total trials}} C _{\text{exactly n}} \cdot p(success) ^{\text{ trials successful}} \cdot p (fail)^{(\text{trials left})} \\ $
$ _{\text{4}} C _{\text{2}} \cdot p(odd) ^{\text{2}} \cdot p (even)^{(\text{2})} \\ _{\text{4}} C _{\text{2}} \cdot p \left( \frac{2}{3} \right) ^{\text{2}} \cdot p \left( \frac{1}{3} \right)^{(\text{2})} \\ \red 6 \cdot p \left( \frac{2}{3} \right) ^{\text{2}} \cdot p \left( \frac{1}{3} \right)^{(\text{2})} \\ 6 \cdot \red{ \frac 4 9} \cdot \red{\frac 1 9 } \\ \frac {24}{81} $
Problem 2
Problem 3
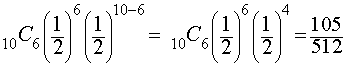
Problem 4
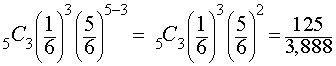
Problem 5
$ _{\blue{ \text{total trials}}} C _{\red n} \cdot p( \text{success} ) ^{\red n} \cdot p (fail)^{\blue {total} - \red n } \\ $
$ _{\blue{ \text{5}}} C _{\red 2} \cdot \left( \frac{ 1 }{ 6 } \right) ^{\red 2} \cdot \left( \frac{ 5 }{ 6 } \right)^{\blue 5 - \red 2} \\ 10 \cdot \left( \frac{ 1 }{ 6 } \right) ^ 2 \cdot \left( \frac{ 5 }{ 6 } \right)^{3} \\ 10 \cdot \left( \frac{ 1 }{ 36 } \right) \cdot \left( \frac{ 125 }{ 216 } \right) \\ \frac{ 1,250 }{ 7716 } $
