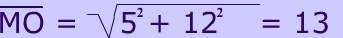-
This Page:
- Diagonal Related:
- Properties of parallelograms
- Is a square a rectangle?
- square
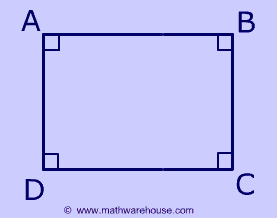
A rectangle is a parallelogram with 4 right angles. Now, since a rectangle is a parallelogram, its opposite sides must be congruent and it must satisfy all other properties of parallelograms
The Properties of a Rectangle
4 Right Angles
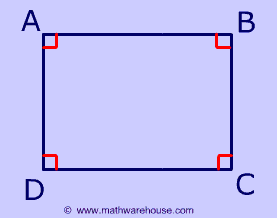
In a rectangle, all angles are 90°
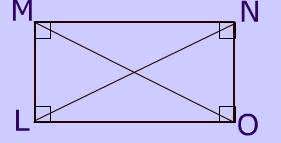
Diagonals of Rectangle
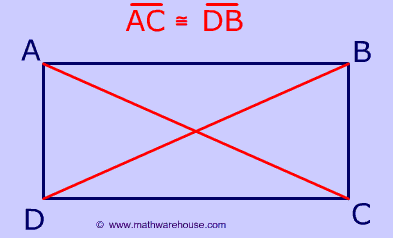
The diagonals of a rectangle are congruent.
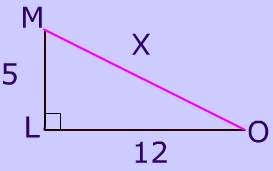
It's easy to prove that the diagonals of a rectangle with the Pythagorean theorem. Click here to see the proof.
Practice Problems
-
This Page:
- Diagonal Related:
- Properties of parallelograms
- Is a square a rectangle?
- square
Problem 1
In rectangle STAR below, SA =5, what is the length of RT?
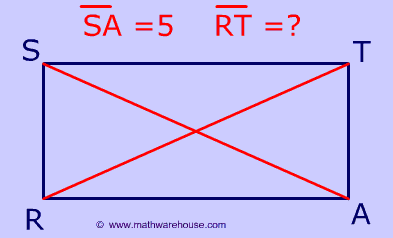
Since the diagonals of a rectangle are congruent, RT has the same length as SA.
Therefore, RT = 5
Problem 2
If side MN = 12 and side ML = 5, what is the length of the other two sides?
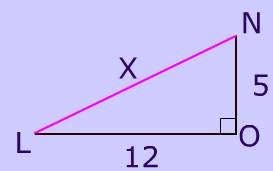
Side LO = 12 and NO = 5
Remember that a rectangle is a parallelogram, so it has all of the properties of parallelograms , including congruent opposite sides.
Problem 3
How Long is MO and MZ in the rectangle pictured on the left?
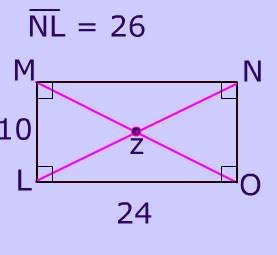
Since the diagonals of a rectangle are congruent MO = 26.
Finding length of MZTo find MZ, you must remember that the diagonals of a parallelogram bisect each other.(Remember a rectangle is a type of parallelogram so rectangles get all of the parallelogram properties)
If MO = 26 and the diagonals bisect each other, then MZ = ½(26) = 13
$$ \angle SZT $$ and $$ \angle SZA $$ are supplementary angles,
Therefore $$ \angle SZA = 120° $$
Next, remember that the diagonals of any parallelogram bisect each other and the diagonals of a rectangle are congruent.
Therefore, SZ = AZ, making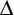 
SZA isosceles and $$ \angle $$ZSA
$$ \angle $$ZAS, being base angles of an isosceles triangle. Therefore, x = 30 °
