Quick Overview
- If two functions squeeze together at a particular point, then any function trapped between them will get squeezed to that same point.
- The Squeeze Theorem deals with limit values, rather than function values.
- The Squeeze Theorem is sometimes called the Sandwich Theorem or the Pinch Theorem.
Graphical Example
In the graph below, the lower and upper functions have the same limit value at $$x = a$$. The middle function has the same limit value because it is trapped between the two outer functions.
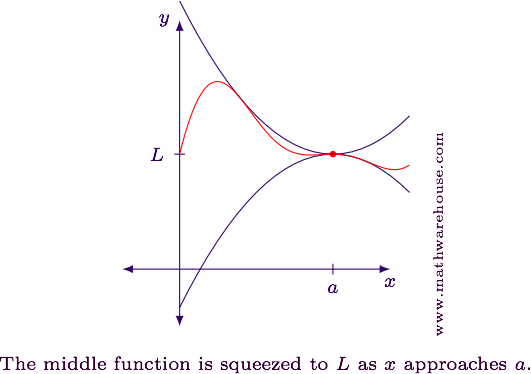
Formal Statement
Suppose $$f(x) \leq g(x) \leq h(x)$$ for all $$x$$ in an open interval about $$a$$ (except possibly at $$a$$ itself). Further, suppose
$$\displaystyle\lim_{x\to a} f(x) = \lim_{x\to a} h(x) = L$$
Then, $$\displaystyle\lim\limits_{x\to a} g(x) = L$$
Note that the exception mentioned in the statement of the theorem is because we are dealing with limits. That means we're not looking at what happens at $$x = a$$, just what happens close by.
Example 1
Suppose there are three functions such that $$f(x)\leq g(x) \leq h(x)$$ when $$x$$ is near $$2$$.
Further, suppose $$f(x) =-\frac 1 3 x^3+x^2-\frac 7 3$$ and $$h(x) = \cos\left (\frac \pi 2 x\right)$$ (with $$x$$ measured in radians).
Determine $$\displaystyle\lim\limits_{x\to 2} g(x)$$
Solution
Find $$\displaystyle\lim\limits_{x\to 2} f(x)$$
$$ \begin{align*} \displaystyle\lim_{x\to 2} f(x) & = \lim_{x\to 2}\left(-\frac 1 3 x^3+x^2-\frac 7 3\right)\\[6pt] & = \left(-\frac 1 3 (2)^3+(2)^2-\frac 7 3\right)\\[6pt] & = \left(-\frac 8 3+4-\frac 7 3\right)\\[6pt] & = -1 \end{align*} $$
Find $$\displaystyle\lim\limits_{x\to 2} h(x)$$
$$ \begin{align*} \lim_{x\to 2} h(x) & = \lim_{x\to 2} \cos\left(\frac \pi 2 x\right)\\[6pt] & = \cos\left(\frac \pi 2 (2)\right)\\[6pt] & = \cos\left(\pi\right)\\[6pt] & = -1 \end{align*} $$
Since $$f(x) \leq g(x) \leq h(x)$$ and $$\displaystyle\lim\limits_{x\to 2} f(x) = \displaystyle\lim\limits_{x\to 2} h(x) = -1$$, the Squeeze Theorem guarantees $$\displaystyle\lim\limits_{x\to 2} g(x) = -1$$ as well.
$$\displaystyle\lim\limits_{x\to 2} g(x) = -1$$
Example 2
Suppose there is a function, $$g(x)$$, such that $$f(x)\leq g(x)\leq h(x)$$ when $$x$$ is near $$-1$$.
Further, suppose $$f(x) =-\frac 1 4 x^2-\frac 1 2 x$$ and $$h(x) = \frac 1 3 x^2 + \frac 2 3 x + \frac 2 3$$
Determine $$\displaystyle\lim\limits_{x\to-1} g(x)$$.
Solution
Determine $$\displaystyle\lim\limits_{x\to-1} f(x)$$
$$ \\ \begin{align*} \displaystyle\lim_{x\to-1} f(x) & = \displaystyle\lim_{x\to-1} \left(-\frac 1 4 x^2-\frac 1 2 x\right)\\[6pt] & = -\frac 1 4(-1)^2-\frac 1 2(-1)\\[6pt] & = -\frac 1 4 + \frac 1 2\\[6pt] & = \frac 1 4 \end{align*} \\ $$
Determine $$\displaystyle\lim\limits_{x\to -1} h(x)$$
$$ \\ \begin{align*} \displaystyle\lim_{x\to-1} h(x) & = \displaystyle\lim_{x\to-1} \left(\frac 1 3 x^2 + \frac 2 3 x + \frac 2 3\right)\\[6pt] & = \frac 1 3(-1)^2 + \frac 2 3(-1) + \frac 2 3\\[6pt] & = \frac 1 3 - \frac 2 3 + \frac 2 3\\[6pt] & = \frac 1 3 \end{align*} \\ $$
The two outer functions, $$f$$ and $$h$$, don't squeeze together (that is, their limits are different). Consequently, the most we can say about $$\displaystyle\lim\limits_{x\to-1} g(x)$$ is that it is somewhere between $$y = \frac 1 4$$ and $$y = \frac 1 3$$ if it exists at all.
$$\displaystyle\lim\limits_{x\to-1} g(x)$$ is indeterminate with the information provided.
The next few lessons will center around this and similar limits. The derivation shown below uses the Squeeze Theorem as well as some basic geometry and trigonometry.
Solution
Step 1Some preliminary information you should recall.
- When angles are measured in radians, the length of a circular arc is $$s = r\theta$$ (link). On the unit-circle, this reduces to $$s = \theta$$.
- For points on the unit-circle, their $$y$$-coordinates are simply $$\sin\theta$$.
Show that $$\sin \theta \leq \theta$$
In the image below, the length of the $${\color{secondaryColor}circular}$$ $${\color{secondaryColor}arc}$$, $${\color{secondaryColor}s = \theta}$$ is larger than the $${\color{importantColor}vertical}$$ $${\color{importantColor}line}$$ $${\color{importantColor}segment}$$, $${\color{importantColor}\sin \theta}$$ that reaches to the point on the circle.
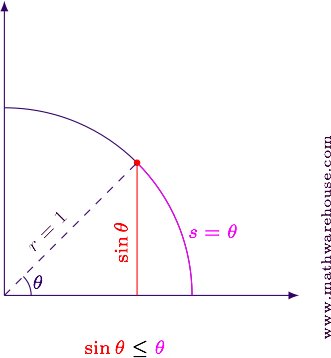
This will be true for any angle $$\theta$$ since the arc must cover the same vertical distance as the line, but also extra horizontal distance as well.
Step 3Show that $${\color{secondaryColor}\theta} \leq {\color{tertiaryColor}\tan \theta}$$
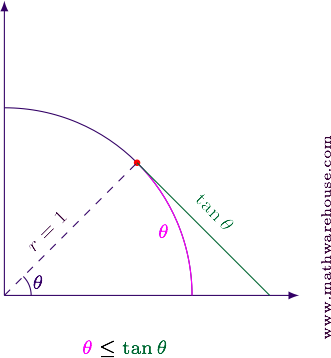
The same reasoning as in Step 1 leads to this conclusion as well. The $${\color{tertiaryColor}diagonal}$$ $${\color{tertiaryColor}line}$$ $${\color{tertiaryColor}segment}$$, $${\color{tertiaryColor}\tan \theta}$$ must cover the same vertical distance as the $${\color{secondaryColor}circular}$$ $${\color{secondaryColor}arc}$$, $${\color{secondaryColor}\theta}$$, but it also must cover a greater horizontal distance. To do this, it must be longer than the arc.
Step 4Algebraically adjust the two inequalities so that we have $$\frac{\sin \theta} \theta$$ in the center.
$$ \\ \begin{align*} {\color{importantColor}\sin \theta} & \leq {\color{secondaryColor}\theta} \leq {\color{tertiaryColor}\tan\theta}\\[6pt] {\color{importantColor}\sin \theta} & \leq {\color{secondaryColor}\theta} \leq {\color{tertiaryColor}\frac{\sin\theta}{\cos\theta}}\\[6pt] {\color{importantColor}\frac{\sin \theta}{\sin\theta}} & \leq {\color{secondaryColor}\frac{\theta}{\sin\theta}} \leq {\color{tertiaryColor}\frac{\sin\theta}{\cos\theta}\cdot \frac 1 {\sin\theta}}\\[6pt] {\color{importantColor}1} & \leq {\color{secondaryColor}\frac \theta {\sin \theta}} \leq {\color{tertiaryColor}\frac 1 {\cos \theta}}\\[6pt] {\color{importantColor}1} & \leq {\color{secondaryColor}\frac {\sin \theta}\theta} \leq {\color{tertiaryColor}\cos \theta}\\[6pt] \end{align*} \\ $$
Step 5Find the limit as $$x\to 0$$ for the two outer functions.
$${\color{importantColor}\displaystyle\lim_{\theta \to 0} 1} = {\color{tertiaryColor}\displaystyle\lim_{\theta \to 0} \cos \theta} = 1$$
Step 6Use the Squeeze Theorem
Since $$y = \frac{\sin\theta}\theta$$ is trapped between $$y = 1$$ and $$y = \cos \theta$$, we can use the squeeze theorem to conclude that $$\displaystyle\lim\limits_{\theta\to0}\frac{\sin\theta}\theta = 1$$.
Answer$$\displaystyle\lim\limits_{\theta\to 0} \frac{\sin \theta} \theta = 1$$


















