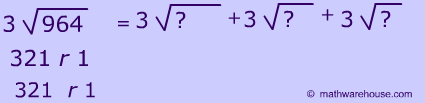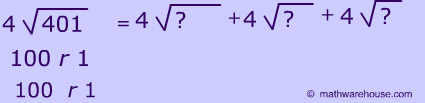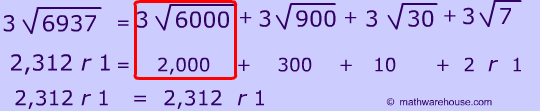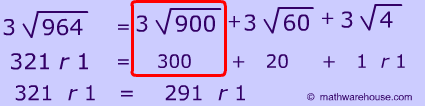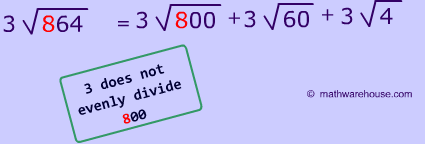A Starting Example
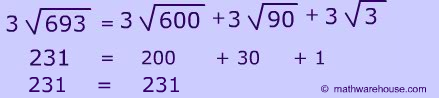
As the above example of long division shows, we can "split up" the dividend (693) into a sum and distribute our division, one by one over each part.
Problem 1
In this case, we split up the dividend 964 into 900 + 60 + 4, and we divide each part by 3, then at, the end we sum them all up.
Problem 2
In this case, we split up the dividend 401 into 400 + 0 + 1, and we divide each part by 4, then at, the end we sum them all up.
Problem 3
In this case, we split up the dividend 6,937 into 6000 + 900 + 30 + 7, and we divide each part by 3, then at, the end we sum them all up.
What about carrying?
All of the problems that we have done so far have not involved carrying remainders from one part to the next.
For instance, in the prior problem $$ 6837 \div 3 $$, our divisor 3 evenly divided into the following parts.
- $$ 6,000 \div 3 $$ gives us the nice even quotient of 2,000.
- $$ 900 \div 3 $$ yields 300.
- $$ 30 \div 3 $$ yields 10.
It's not till the very last part of 7 that a remainder comes into play. The same thing occurs with the first problem that we did.
Or look at the first problem we did, our divisor 3 evenly divided into each part. $$ 900 \div 3 $$ gives us the nice even quotient of 300 and $$ 600 \div 3 $$ yields 200 exactly etc..
What if we change one digit?
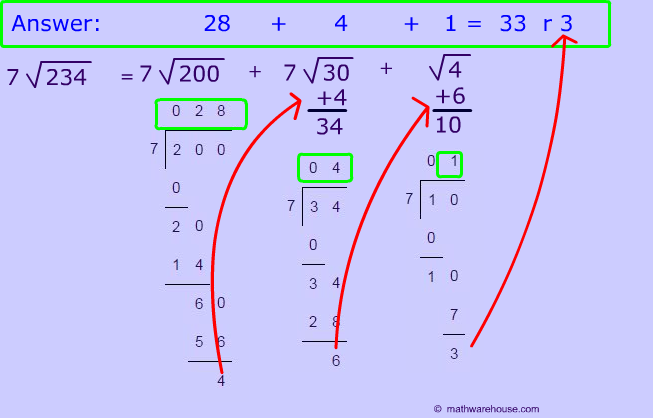
We are going to change the first digit , from our first problem, by one.
Problem 4 (with carrying)
Let's take our old question 1 and change the first digit. How should we approach this now?
Problem 5
Answer:
Problem 6
Answer:
Problem 7
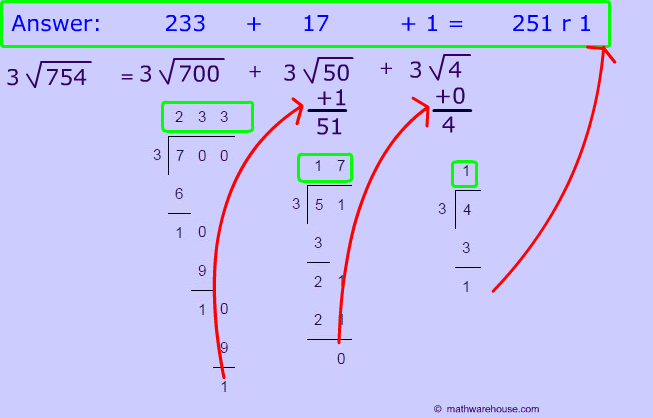
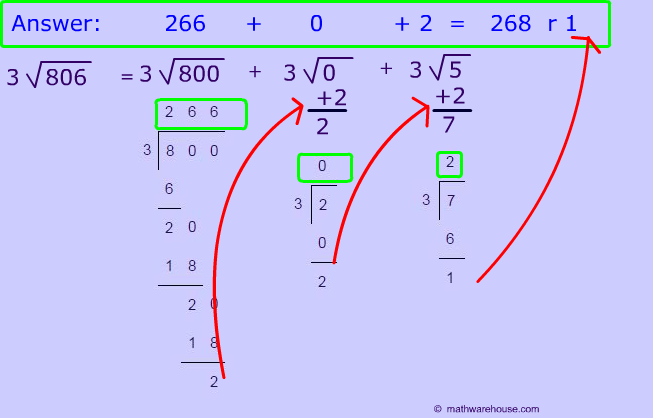
Answer:
This page is dedicated to parents or other adults (like the owner of this website) who are trying to help younger kids learn how to work with some of the newer ways that schools are teaching kids to do traditional long division and work with numbers.
