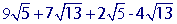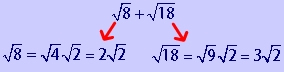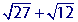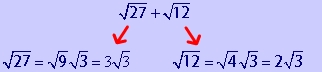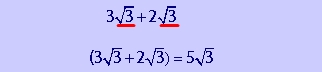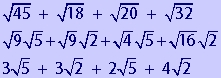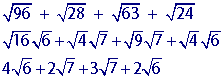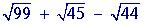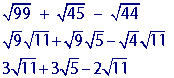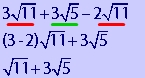The radicand refers to the number under the radical sign. In the radical below, the radicand is the number '5'.

How to Add Simplified Square Roots?
Let's look at the following example.
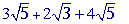
You can only add square roots (or radicals) that have the same radicand . So in the example above you can add the first and the last terms:
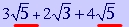
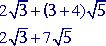
The same rule goes for subtracting. Consider the following example:
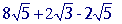
You can subtract square roots with the same radicand --which is the first and last terms.
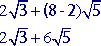
Practice Problems
Directions: Add the square roots below.
Problem 1
Problem 2
Remember -- the same rule applies to subtracting square roots -- the radicands must be the same.
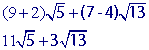
How to Add Square Roots- that are not simplified
Let's look at the following example.
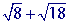
You may immediately see the problem here: The radicands are not the same. Therefore, we can not add them at the moment. However, if we simplify the square roots first, we will be able to add them. Let's use this example problem to illustrate the general steps for adding square roots.
Step 1 Step 1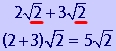
Problem 3
Problem 4
Add square roots with the same radicands.
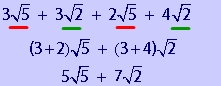
Problem 5
Add square roots with the same radicands.
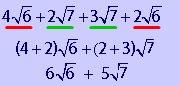
Problem 6
How to Add Square Roots with coefficients?
Let's look at the following example.

Do you see what distinguishes this expression from the last several problems?
Each square root has a coefficent . The rules for adding square roots with coefficients are very similar to what we just practiced in the last several problems -- with 1 additional step --which is to multiply the coefficeints with the simplified square root.
Step 1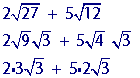
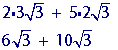
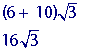
Problem 7
Ignore the coefficients (4 and 5) and simplify each square root.

Multiply the coefficients (4 and 5) by any numbers that 'got out' of the square root (3 and 2, respectively).

Add any radicals with the same radicand.