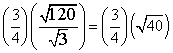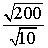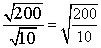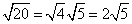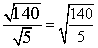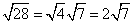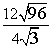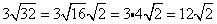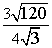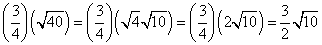Dividing Square Roots

How to divide square roots--with examples

---

Dividing Radicals (square roots) worksheet(Free 25 question worksheet with answer key on this page's topic)

Radicals and Square Roots Home| Scientific Calculator with Square Root

---

Vocabulary Refresher
The radicand refers to the number under the radical sign. In the radical below, the radicand is the number '5'.

Refresher on an important rule involving dividing square roots:

The rule explained below is a critical part of how we are going to divide square roots so make sure you take a second to brush up on this. (Or learn it for the first time;)

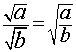
	When you divide two square roots you can "put" both the numerator and denominator inside the same square root. Below is an example of this rule using numbers
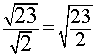
	As you can see the '23' and the '2' can be rewritten inside the same radical sign.

Examples of Dividing Square Roots

Example 1

Step 1) Combine square roots under 1 radicand
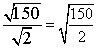
Step 2) Divide (if possible). Since 150 is divisible by 2, we can do this.
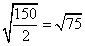
Step 3) Simplify the radical (if possible)

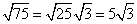
Example 2

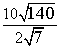Step 1) Rewrite the expression by combining the rational and irrational numbers into two distinct quotients.
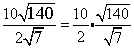
Step 2) Combine the square roots under 1 radicand
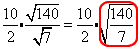
Step 3) Divide the square roots and the rational numbers.
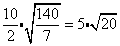
Step 4) Simplify the radical (if possible)

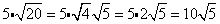
Practice Dividing Square Roots

Directions: Divide the square roots and express your answer in simplest radical form

Problem 1)

Step 1

This problem is like example 1.

Step 1) Combine square roots under 1 radicand

Step 2

Step 2) Divide (if possible). Since 200 is divisible by 10, we can do this.

Step 3

Step 3) Simplify the radical

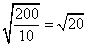
Problem 2)

Step 1

This problem is like example 1.

Step 1) Combine square roots under 1 radicand

Step 2

Step 2) Divide (if possible). Since 140 is divisible by 5, we can do this.

Step 3

Step 3) Simplify the square root

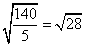
Problem 3)

Step 1

This problem is like example 2.

Step 1) Rewrite the expression by combining the rational and irrational numbers into two distinct quotients.

Step 2

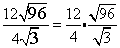
Step 2) Combine the square roots under 1 radicand

Step 3

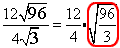
Step 3) Divide the square roots and the rational numbers.

Step 4

Step 4) Simplify the square root

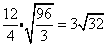
Problem 4)

Step 1

This problem is like example 2.

Step 1) Rewrite the expression by combining the rational and irrational numbers into two distinct quotients.

Step 2

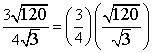
Step 2) Combine the square roots under 1 radicand

Step 3

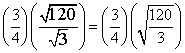
Step 3) Divide the square roots and the rational numbers.

Step 4

Step 4) Simplify the square root