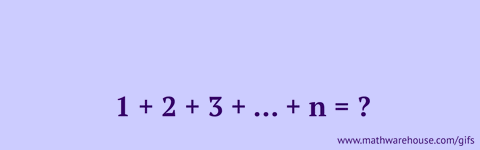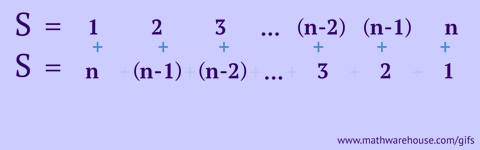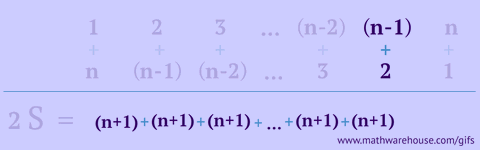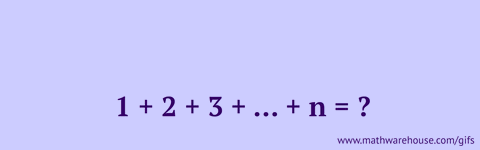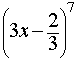The binomial theorem states a formula for expressing the powers of sums. The most succinct version of this formula is shown immediately below.
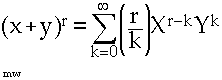
Isaac Newton wrote a generalized form of the Binomial Theorem. However, for quite some time Pascal's Triangle had been well known as a way to expand binomials (Ironically enough, Pascal of the 17th century was not the first person to know about Pascal's triangle)
A closer look at the Binomial Theorem
The easiest way to understand the binomial theorem is to first just look at the pattern of polynomial expansions below.
- (x + y)2 = x2 + 2xy + y2
- (x + y)3 = x3 + 3x2y + 3xy2 + y3
- (x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
Binomial Theorem Formula
The generalized formula for the pattern above is known as the binomial theorem
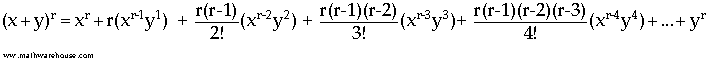
Practice Problems
on the Binomial Theorem
Problem 1
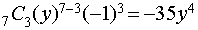
Problem 2
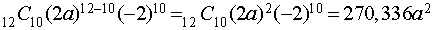
Problem 3
Use the binomial theorem formula to determine the fourth term in the expansion
$$
_7 C _3 (3x)^{7-3} \left( -\frac{2}{3}\right)^3
\\
35 (3x)^4 \cdot \frac{-8}{27}
\\\
35 \cdot 3^3 \cdot 3x^4 \cdot \frac{-8}{27}
\\
35 \cdot 27 \cdot 3 x^4 \cdot \frac{-8}{27}
\\
35 \cdot \cancel{\color{red}{27}} 3x^4 \cdot \frac{-8}{ \cancel{\color{red}{27}} }
\\
\boxed{-840 x^4}
$$
Problem 4
The number of terms in $$\left(a+b\right)^{n} $$ or in $$\left(a-b\right)^{n} $$ is always equal to n + 1. Therefore, when n is an even number, then the number of the terms is (n + 1), which is an odd number.
When the number of terms is odd, then there is a middle term in the expansion in which the exponents of a and b are the same.
Only in (a) and (d), there are terms in which the exponents of the factors are the same.
Problem 5
Step 1
Third term:
$$a_{3} =\left(\frac{5!}{2!3!} \right)\left(a^{3} \right)\left(-\sqrt{2} \right)^{2} $$
Step 2
Expand the coefficient.
$$a_{3} =\left(\frac{4\times 5\times 3!}{2\times 3!} \right)\left(a^{3} \right)\left(-\sqrt{2} \right)^{2} $$
Step 3
Replace $$\left(-\sqrt{2} \right)^{2} $$ by 2. Divide the denominator and numerator by 2 and 3!.
$$a_{3} =\left(2\times 5\right)\left(a^{3} \right)\left(2\right) $$
Step 4
Multiply the coefficients.
$$a_{3} =40a^{3} $$
Problem 6
The binomial has two properties that can help us to determine the coefficients of the remaining terms.
- The variables m and n do not have numerical coefficients. So, the given numbers are the outcome of calculating the coefficient formula for each term.
- The power of the binomial is 9. Therefore, the number of terms is 9 + 1 = 10.
Now, we have the coefficients of the first five terms. By the binomial formula, when the number of terms is even, then coefficients of each two terms that are at the same distance from the middle of the terms are the same. So, starting from left, the coefficients would be as follows for all the terms:
$$1, 9, 36, 84, 126 | 126, 84, 36, 9, 1$$
Problem 7
Step 1
Fourth term:
$$a_{4} =\left(\frac{6!}{3!3!} \right)\left(\frac{a}{b} \right)^{3} \left(\frac{b}{a} \right)^{3} $$
Step 2
Expand the coefficient, and apply the exponents.
$$a_{4} =\left(\frac{4\times 5\times 6\times 3!}{2\times 3\times 3!} \right)\left(\frac{a^{3} }{b^{3} } \right)\left(\frac{b^{3} }{a^{3} } \right) $$
Step 3
Divide the denominator and numerator by 3! and 6.
$$a_{4} =\left(4\times 5\right)\left(\frac{a^{3} }{b^{3} } \right)\left(\frac{b^{3} }{a^{3} } \right) $$
Step 4
Divide denominators and numerators by a$${}^{3}$$ and b$${}^{3}$$.
$$a_{4} =\left(4\times 5\right)\left(\frac{1}{1} \right)\left(\frac{1}{1} \right) $$
Step 5
Multiply the coefficients.
$$a_{4} =20 $$
Problem 8
Step 1
Solution:
$$a_{4} =\frac{6!}{2!\left(6-2\right)!} \left(a^{4} \right)\left(2^{2} \right) $$
Step 2
Expand the coefficient.
$$a_{4} =\frac{5\times 6\times 4!}{\left(2\right)\left(4!\right)} \left(a^{4} \right)\left(4\right) $$
Step 3
Divide the denominator and numerator by 2 and 4!.
$$a_{4} =\left(5\times 3\right)\left(a^{4} \right)\left(4\right) $$
Step 4
Multiply the coefficients.
$$a_{4} =60a^{4} $$
Therefore, the coefficient of $$a{}^{4}$$ is $$60$$.
Problem 9
Step 1
Fourth term of the first binomial:
$$a_{4} =\left(\frac{6!}{3!3!} \right)\left(a^{4} \right)\left(1\right)^{2} $$
Step 2
Expand the coefficient.
$$a_{4} =\left(\frac{4\times 5\times 6\times 3!}{2\times 3\times 3!} \right)\left(a^{4} \right)\left(1\right) $$
Step 3
Divide the denominator and numerator by 6 and 3!.
$$a_{4} =20a^{4} $$
Step 4
Third term of the second binomial:
$$a_{3} =\left(\frac{7!}{2!5!} \right)\left(a^{5} \right)\left(1\right)^{2} $$
Step 5
Expand the coefficient.
$$a_{3} =\left(\frac{6\times 7\times 5!}{2\times 5!} \right)\left(a^{5} \right)\left(1\right) $$
Step 6
Divide the denominator and numerator by 2 and 5!.
$$a_{3} =21a^{5} $$
Step 7
Sum of terms =
$$20a^{4} +21a^{5} $$
Problem 10
Step 1
The expansion of this expression has 5 + 1 = 6 terms. So, the two middle terms are the third and the fourth terms.
Use the formula.
$$ a_{3} =\left(\frac{5!}{2!3!} \right)\left(8a^{3} \right)\left(9\right) $$
Step 2
Replace 5! = 4 $$\times$$ 5 $$\times$$ 3!, and 2! = 2.
$$a_{3} =\left(\frac{4\times 5\times 3!}{2\times 3!} \right)\left(8a^{3} \right)\left(9\right) $$
Step 3
Divide the denominator and numerator by 3! and 2.
$$a_{3} =\left(10\right)\left(8a^{3} \right)\left(9\right) $$
Step 4
Multiply all the coefficients.
$$a_{3} =720a^{4} $$
Step 5
The next term is
$$a_{4} =\left(\frac{5!}{2!3!} \right)\left(a^{2} \right)\left(-27\right) $$
Step 6
Replace 5! = 4 $$\times$$5 $$\times$$ 3!, and 2! = 2.
$$a_{4} =\left(\frac{4\times 5\times 3!}{3!2!} \right)\left(4a^{2} \right)\left(27\right) $$
Step 7
Divide the denominator and numerator by 3! and 2.
$$a_{4} =\left(10\right)\left(4a^{2} \right)\left(27\right) $$
Step 8
Multiply all the coefficients.
$$a_{4} =1080a^{2} $$
