Systems of Linear Inequalities, Solutions of these Systems. Pictures, examples and practice problems.

A System of linear inequalities is simply two or more linear inequalities on the same plane. In other words, a system of linear inequalities is just two or more inequalities together.

The easiest way to remember what 'system' means in this context is by answering the following question: 'Does the word system ever refer to just one thing or does system always refer to more than one thing?'

The answer is 'more than one thing' Likewise a 'system of linear inequalities' is 'more than one linear inequality'.

Interactive System
of Linear Inequalities

Click and drag on the points below and the system of linear inequalities will adjust accordingly. (Full sized interactive system of linear inequalities)

Snap to grid

Y ≥ X ≥

Use it to enable or disable snapping

Click on the equation to change inequality type between ≤, <, > and ≥

You can drag the points to change the line equation

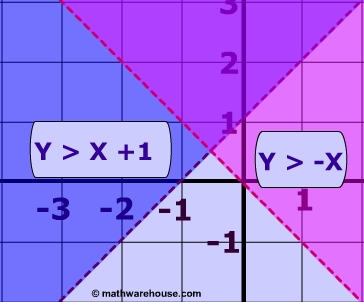
Below are the graphs of the linear inequalities: y < x + 1 and y > x.

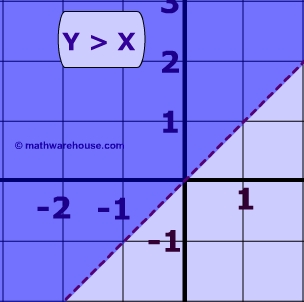
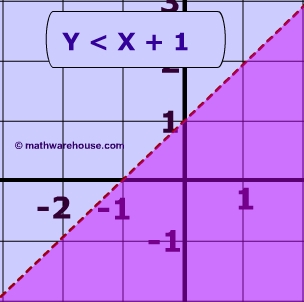
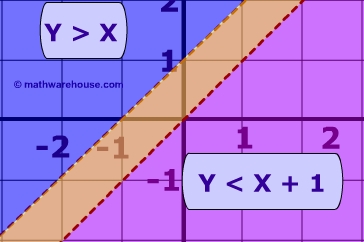
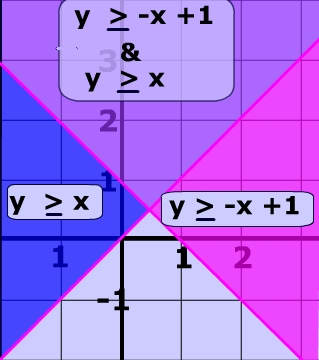
Pictured above is the system of inequalities made up the same two linear inequalities:

y < x + 1
y > x

When we take both of the linear inequalities pictured above and graph them on same Cartesian plane, we get a system of linear inequalities. The solution of this system is the yellow region which is the area of overlap. In other words, the solution of the system is the region where both inequalities are true. The y coordinates of all points in the yellow region are both greater than x + 1 as well as less than x.