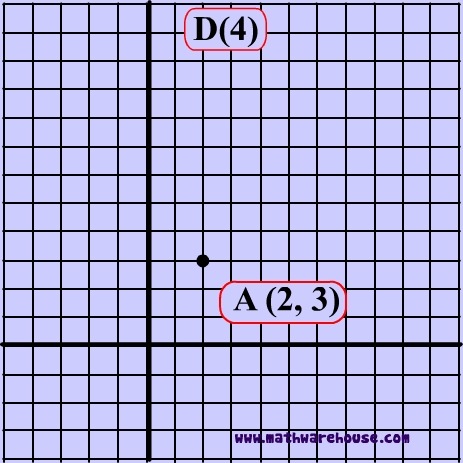
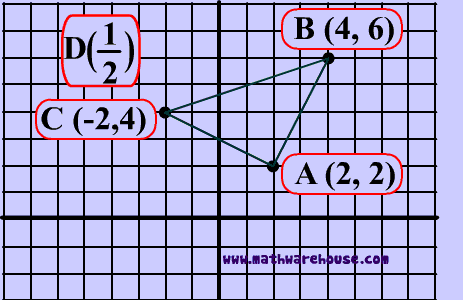
What is a Dilation?
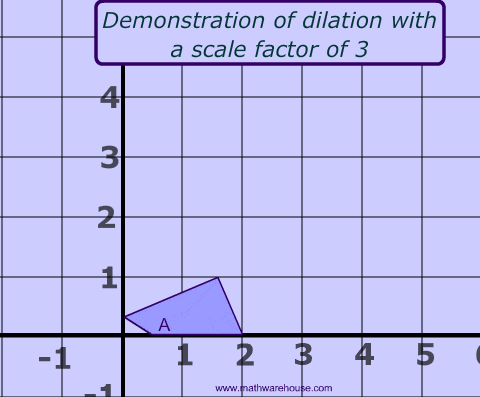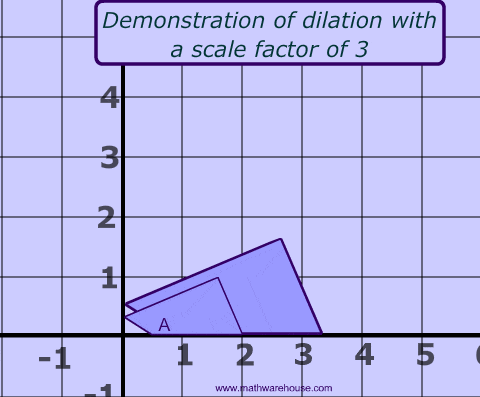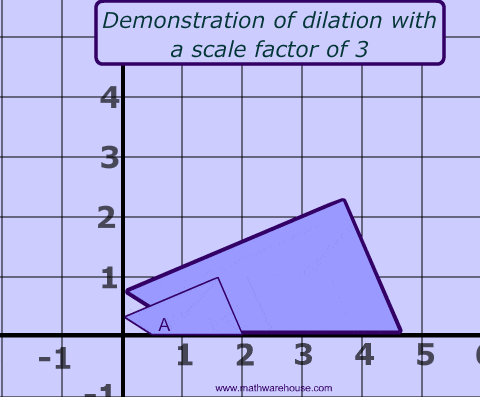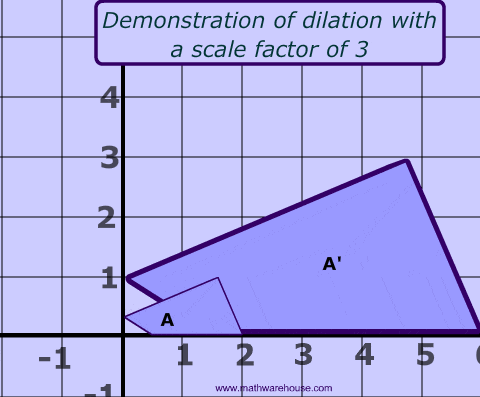
A dilation is a type of transformation that changes the size of the image. The scale factor, sometimes called the scalar factor, measures how much larger or smaller the image is. Below is a picture of each type of dilation (one that gets larger and one that gest smaller).
Example 1
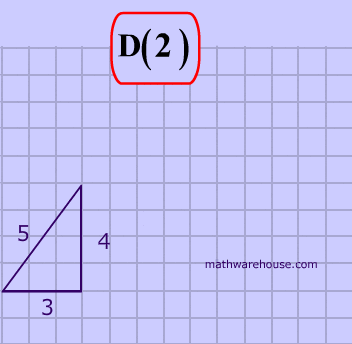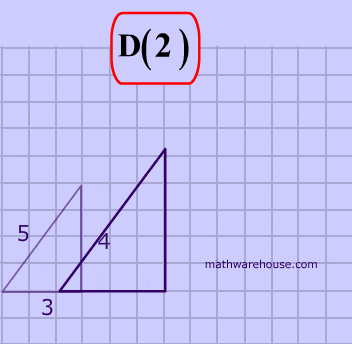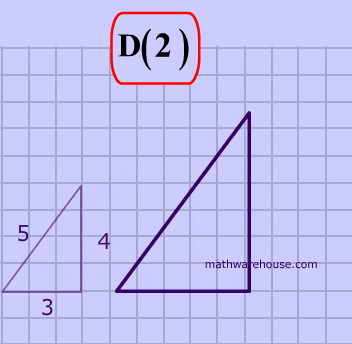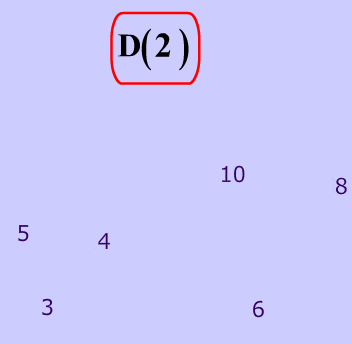
The picture below shows a dilation with a scale factor of 2. This means that the image, A', is twice as large as the pre-image A. Like other transformations, prime notation is used to distinguish the image fromthe pre-image. The image always has a prime after the letter such as A'.
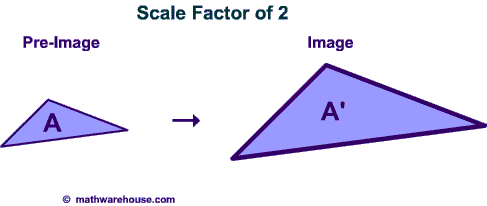
Example 2
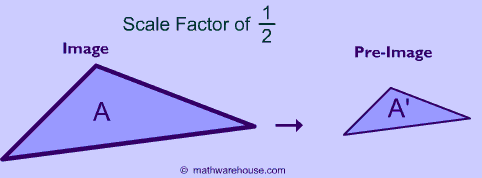
Dilations can also reduce the size of shape. The picture below demonstrations a dilation of $$ \frac{1}{2}$$ Any time that the scale factor is a fraction, the image will get smaller.