In (7.SP.C.6), the Common Core State Standards for Mathematics reads ‘Approximate the probability of a chance event by collecting data on the chance process that produces it and observing its long-run relative frequency, and predict the approximate relative frequency given the probability. For example, when rolling a number cube 600 times, predict that a 3 or 6 would be rolled roughly 200 times, but probably not exactly 200 times.’
Theoretical and Experimental Probability Lesson Plan 7th Grade
Discussion/Introduction
Probability is the study of what will “probably” happen based upon a mathematical perception of “chance”. For this lesson, we will be doing some foundational thinking using independent events to compare and contrast theoretical and experimental probability.
Objective
- Students will be able to find the theoretical probability of an event and then test it against an example of experimental probability.
- Students will be able to understand that the theoretical probability predictions should be closer to the actual experimental probability results as the number of trials increases.
Supplies
- A coin
- Theoretical Probability Worksheet (download printable)
- Dice (1 for each student)
- Calculators (optional)
Methodology/Procedure
- Bring up two students for a “gambling” opportunity. Ask each student to pick a side of the coin (heads or tails). Inform them that the first student to get 5 of their side (heads or tails) will be the winner. Ask the following questions before they start:
- How many flips of the coin do you think it will take before we have a winner?
- Does Student #1 have an equal chance of winning as Student #2?
- Can any of you summarize Student #1’s chance of winning? Student #2?
- Tally their data in a table such as this. Keep this table visible when doing steps 3 and 4 (to compare and contrast).
| Student #1’s Name | Heads | |
| Student #2’s Name | Tails |
- Bring up a second partnership to flip coins. Inform them that the first student to get 10 of their side (heads or tails) will be the winner. Ask the same questions used before.
- Tally their data in a table just like you did with Step 2.
- Ask the following post-coin flip questions (they may need to be altered depending on how the “coin flipping battles” went):
- Why did it not take exactly 9 coin tosses to get a winner in our first battle?
- Why did it not take exactly 19 coin tosses to get a winner in our second battle?
- If I flipped a head the first time, does that mean that I will always flip a tail the next time? Am I more likely to flip a head if I just flipped a head?
- What was my probability of flipping a head each coin toss?
- What was my probability of flipping a tail each coin toss?
- Bring up two more volunteers. This time bring out a die (singular of dice). Do “rock, paper, scissors” to decide who gets to be the student that gets the factors of 6 and who gets to be the student that gets the non-factors of 6. They will have very different probability. Whenever one of their numbers is rolled, they get a tally mark. The winner has 10 tally marks.
- How many rolls of the die do you think it will take before we have a winner?
- Does Student #1 have an equal chance of winning as Student #2?
- Can any of you summarize Student #1’s chance of winning? Student #2?
- Tally their data in a table such as this.
| Student #1’s Name | Factors of 6 (1, 2, 3, 6) | |
| Student #2’s Name | Non-Factors of 6 (4, 5) |
- Discuss this die rolling example.
- Were we close in our prediction of how many rolls we thought it would take?
- What was Student 1’s probability of winning written as a percent? (a great opportunity to show how to convert to percents)
- What percent of the rolls did Student 1 have? (a great opportunity to show how to convert to percents)
- Hand out the Theoretical Probability Worksheet and a die (singular of dice) to each student. Explain the worksheet to the students. Here’s an image of part of the worksheet.
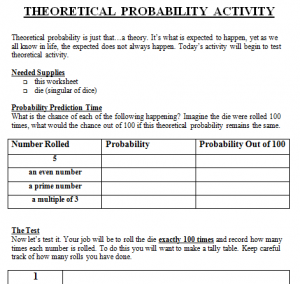
- Fill in the “Probability Prediction Time” section with the students. Teach the students how to tally in groups of 5 (this will be new to some). The biggest challenge in this activity is having students roll the dice exactly 100 times. You may want to put them into partnerships instead. In this case, one student keeps track of the number of rolls while the other student tallies his/her results. Then switch so that each student has his/her own unique data. If you are not using partners, really stress to the students that they will want to organize their total number of rolls somehow (either through tallying on their own) or stopping to count their progress regularly throughout. Each student needs exactly 100 rolls for this to be highly successful. Have the students complete “The Test” section of the worksheet.
- Note: This will get loud as students roll. I usually give about 5-10 minutes for the actual 100 rolls and tallying time. If you are using partners to help with counting the rolls, then double the time needed.
- As a class, complete the “Comparing Theory with Reality” section of the worksheet. Students may need help turning their fractions into percents for the “Probability Out of 100” column. You may opt to let them use calculators.
- Have students independently answer the “Critical Thinking” questions.
- As a good follow up, you can choose one of the categories (i.e. multiples of 3) and come up with a class total for this to show that the greater the number of trials, the closer the experimental probability results come to the theoretical probability predictions. To do this, you would find the sum of all multiples of 3 (as an example) for the class. You can do this more efficiently by collecting class table sums. Then take this sum and divide it by 100 times the number of students in this class (the total number of rolls for the class). This will give you a decimal number that you can convert to a percent. It should be fairly close to the theoretical probability predicted percent.
- If time allows, you can do this with the other categories to see how close your class was as a whole for each theoretical probability prediction.
Common Core Standards
CCSS.MATH.CONTENT.7.SP.C.6
Approximate the probability of a chance event by collecting data on the chance process that produces it and observing its long-run relative frequency, and predict the approximate relative frequency given the probability. For example, when rolling a number cube 600 times, predict that a 3 or 6 would be rolled roughly 200 times, but probably not exactly 200 times.
Common Core Standard 3.NF.3 Lesson Plans
Common Core Standard 3.NF.3 Lesson Plans
In 3.NF.3, Third Grade Number and Fractions item 3, the Common Core State Standards for Mathematics reads:
Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
a. Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
b. Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model.
c. Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram.
d. Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
Lesson Plans on This Topic
3rd Grade Lesson Plan: Discovering Equivalence
Discussion/Introduction
What does it mean when a fraction is the same as another, and what does it mean when it is different? Is 2/4 really the same as ½? Although your students have discovered informally that the slab of pie represented by those two fractions— and the point on the number line—looks, feels, and acts the same, they still need to take this one step further and realize that these two fractions are actually one and the same quantity.
This 3rd grade lesson plan will give students the tools they need to understand the concepts of same and different applied to fractions. Through visual ordering exercises your students will become adept at recognizing fractions that are the same, and by the end of today’s session they should be able to make up their own simple lists of equivalent fractions.
Fractions and Ordering: Discovering Equivalence
It’s important that you introduce this topic with real world, dynamic, easily understandable examples rather than with mathematical equations and manipulations. Your students aren’t ready, right now, to grasp that 2/4 is ½ because they can divide 2 out of both sides of that first fraction. That is for later. Introduced with fancy manipulation, fractions become a complicated numerical puzzle that will leave many of your students feeling confused and helpless. When demonstrated with visual examples, though, equivalent fractions will speedily seem intuitive to your students; nothing less than common sense.
Objective
Students will understand that two fractions are equivalent if they are the same size, or the same point on a number line. They will be able to explain why fractions are equivalent, and will be able to recognize and make up lists of simple equivalent fractions.
Supplies
- Folding paper, 1 square per student.
- Flashcard sets; one per student (download printables)
- 2 scrabble tile holders
Methodology/Procedure
As a warmup, begin with a quick fractions review. Pass out the folding paper, and have your students fold fractions—as fast as possible; first one done is the winner—as you call them out. Call out ½, 1/3, ¼, 1/6, and 1/8, in random order.
If they have difficulty, continue this exercise for several rounds. When they achieve fluency, tell them you are proud. Tell them you’ve got a fun topic to look at today; and it’s a topic you won’t even need to teach; they can discover it all themselves. Give each student a partial set of fraction number & visual flashcards; ½, ¼, 2/4, and ¾ cards from both visual and numerical sets. Ask them to match the cards to the pie pictures, and then to order both sets according to size, smallest to largest.
When they have finished, walk around the room and review the students’ work. Help any who have had trouble, encouraging them to look at the picture cards and compare relative sizes. Find two students who have chosen different orderings, and give them the scrabble tile holders. Ask them to place their numerical cards carefully on the tile holder, then go to the front of the room and display their ordering to the class. Observe that these are two different orderings of the same set; ask which is wrong.
Invite any students who point out one or the other as wrong to explain why it is wrong, using the picture flashcards and comparing sizes.
If your students say unanimously that neither is wrong, tell them that they are right. Draw on the board the visual circle fractions, and demonstrate how the two parts are exactly the same.
Tell them that in math the two fractions ½ and 2/4 are called equivalent fractions. Explain that what that means is that they are two names for the same thing. Sometimes one name is more useful, sometimes the other is. Ask them if they know anyone who has two names. If they do not come up with their own examples, remind them of a common acquaintance—the principal, perhaps, who is called Mr. Brown at school, Daddy at home, and Jake by his golfing friends. Point out that the man these names this refers to is the same, no matter what name he is called, and that all of these names belong to him equally.
You can also use yourself as an example.
Draw a half circle on the chalkboard, and tell your students this could be labeled as ½ or 2/4, and both answers would be entirely correct. Ask them if they can think of any other names for this same portion.
If any students have suggestions, invite them to come up and demonstrate equivalence on the board with pictures. If no-one has any idea, use lines to divide the circle on the board into eight equal wedges, and point out that half is also four 1/8 wedges, or 4/8.
Ask your students how many names each portion has. Let them think about and discuss this, and then demonstrate how each portion will have an infinite number of names, because you can always divide the existing pieces each in half again to get twice the amount of smaller pieces.
Hand out the remaining card sets, and ask the students to match the number cards to the visual cards and then order all the cards by portion size, from smallest to largest. Suggest they show equivalence by placing equivalent fractions at the same level in their orderings.
Let your students take their times over their orderings. If they finish quickly and you have time left before the end of the class, do some quiz work: draw shaded portions on the blackboard and ask your students to help you come up with a list of possible ‘names’.
Common Core Standards
This lesson is aligned to standard 3.NF.3 in the Common Core State Standards for Mathematics; 3rd Grade Numbers and Fractions item 3. 3.NF.3 reads, in part:
3.NF. 3. Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
a. Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
b. Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model.
Web Resources/Further Exploration
The beautiful flashcards your students used in this lesson are made with the help of Mathwarehouse’s nifty Visual Fraction applet. This applet is a really fun way to generate classroom graphics, and also an enjoyable way for students who might be having difficulty visualizing fractions to see pizza portions generated before their eyes as they type in the fractions they are curious about.
Multiplying Integers Lesson Plan 7th Grade
Discussion/Introduction
By the time students enter into 7th grade, they hopefully have a strong understanding of multiplication with whole numbers. This lesson introduces multiplication with all integers. I highly recommend spending some time on this concept before introducing multiplication with other negative rational numbers. I have successfully used this lesson with my highly supported math classes. The use of the values -13 through +13, which you will see later in this lesson, makes it obtainable for even those students that may struggle with their math facts.
In preparation for this lesson, I recommend spending some time with students reviewing basic multiplication facts and the reasoning behind multiplication. It is important for students to understand that multiplication is repeating addition.
Objective
- Students will understand the rules for multiplying integers.
- Students will be able to solve two term integer multiplication problems.
Supplies
- Multiplying Integers Intro Packet
- Multiplying Integers Worksheet (with bags of stones on it)
- 26-52 (even number) playing cards for every partnership (or group of 3 depending on structuring of groups)
Methodology/Procedure
- Pass out the Multiplying Integers Intro Packet. Guide the students through the thinking process for Activities #1-4. Here is an image of part of the packet.

- Discuss with the students that there are rules for multiplying and dividing integers. Here are a couple story lines to help the students remember. Really make them dramatic when you teach them.
- The married couple rules—An optimistic person (“I love life! Life is great!”) meets another optimistic person (“I love life too! The butterflies and the birds and everything are just so beautiful!”). Do you think their relationship might work out, that it might be positive? (Student response—yes.) Now imagine an extraordinarily negative person (“I hate life! Life is no good!”) meets another negative person (“I do not like life either! Let us complain about it together!”). Though they may complain about virtually everything, could their relationship still work out? Could it still be positive for them since they see the world in the same way? (Student response—yes.) Now imagine an extraordinarily positive person (“I love life! Life is great!”) meets an extraordinarily negative person (“I hate life! Life is no good!”). Do you think their relationship will work out? (Student answer—no.) No, it will be a negative thing.
- Consequences of one’s actions—When a good thing happens to a good person, that is good. When a good thing happens to a bad person, that is bad. When a bad thing happens to a good person, that is bad. When a bad thing happens to a bad person, that is good.
- After going through one of the story lines, teach the rules of multiplying integers and then complete Activity 5 in the Multiplying Integers Packet.
- For additional practice, or for another approach to understanding multiplication of integers, you may pass out and complete the Multiplying Integers Worksheet with the bags of stones on it. Here is the basic premise of this sheet and an image of part of the worksheet:
- Stones are either cold (-) or hot (+).
- You can either remove (-) or add (+) stones.
- When you remove (-) a cold (-) stone, the temperature goes up (+).
- When you remove (-) a hot (+) stone, the temperature goes down (-).
- When you add (+) a cold (-) stone, the temperature goes down (-).
- When you add (+) a hot (+) stone, the temperature goes up (+).

- As a follow-up, independent practice activity, get students into groups of 2 (or 3 if your class struggles with math facts) for Multiplying Integers War. Pass out 26-52 cards to each group. Groups of 3 have one extra person that acts as the “judge” checking the accuracy of the math facts and may use a multiplication table and/or calculator. Here is how the game is played:
- Each player gets half of the well-shuffled deck.
- Cards are either red (negative) or black (positive). The cards have their face value except for A = 1, J = 11, Q = 12, and K = 13. That means you have the integers from -13 to + 13 in play (except for 0).
- The players flip over the top card on their deck at the same time. The student with the higher valued card gets to attempt the math fact. If the player gets the math fact (sign included) correct, he/she gets both cards. If the player misses the math fact (sign included), then his/her opponent gets both cards.
- If both players play the same card (color and value), then a war ensues and students lay down three face down cards each and then flip for a winner (playing as described above).
- If you have a 3rd person acting as the “judge”, I recommend changing players after 10-15 minutes. The “judge” will then challenge the student that had the most cards (or was winning) at the time of the switch.
- This activity can be followed up by standard multiplication of integers homework.
Common Core Standards
- CCSS.MATH.CONTENT.7.NS.A.2
Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.- CCSS.MATH.CONTENT.7.NS.A.2.A
Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (-1)(-1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts.
- CCSS.MATH.CONTENT.7.NS.A.2.A
Web Resources/Further Exploration
Common Core Standard 7.NS.A.2 Lesson Plans
In (7.NS.A.2), the Common Core State Standards for Mathematics reads ‘Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.’
- CCSS.MATH.CONTENT.7.NS.A.2.A
Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (-1)(-1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts.
Lesson Plans on this Topic
Hopscotch Fractions: Third Grade Lesson Plan
Discussion/Introduction
This lesson plan is meant to follow another; 3rd Grade Fractions on the Number line. These lessons are both aligned to Common Core Standard 3.NF.2. Here I’ll assume you’ve gone through that first lesson, and that your students are comfortable marking off intervals to show 1/b on the number line.
In your last lesson your students will have stayed in their chairs during most of the class period, working hard on dividing up fraction intervals and coming to terms with the idea that 1/b on a number line means portioning the interval between 0 and 1 into b parts and then, starting at zero, marking off one of these parts. Today you get to cement that concept a bit more by taking the next step up: your students will discover that a/b means that, starting at 0, you mentally hop a ‘1/b’ size steps toward 1.
That’s all they need to learn today, but you want them to know it backwards, forwards, and inside-out. Since there’s no better way to get to that point than with a fun de-stressing game, you’ll do this by getting your students up out of their chairs for a rousing game of ‘hopscotch fractions’. Games have a way bringing book learning from the ‘theoretical’ category into ‘real life’, and this one is no exception.
Objective
That students would be comfortable representing a fraction a/b on a number line diagram by marking off a lengths 1/b from zero, and that they’d understand that the resulting interval has size a/b, and that its endpoint locates the number a/b on the number line.
Supplies
- Large 0-2 number lines, laminated and taped to the floor (ideal length: 3 or 4 feet long). These can also be prepared by taping standard printing paper end to end and drawing the number lines with markers, using rulers for uniformity. You’ll need one for every four students.
- Strips of colored paper the same size as one unit on the number line; one per student; four colors.
- A marker for each student; four colors; each student’s marker must be coordinated with his paper.
- Fraction Nametags (download printable)
- Hopscotch Flashcards (download printable; print 1 per page)
- Three types of stickers (ideally, small stars in red, yellow, or green; but other simple colored stickers can substitute).
Methodology/Procedure
Begin by reviewing what you taught in the last lesson. Remind the students that we talked about what fractions of abstract numbers mean, and we learned that they work in exactly the same way as fractions of tangible, concrete things like apples. Draw your 0-2 number line on the board, mark 0, 1, and 2, and ask how you would find out where to mark 1/3. After listening to their suggestions, take a strip of paper the size of a unit on your number line, divide it in thirds, and use that to mark 1/3.
Then ask your students how you’d mark 2/3. Give them permission to discuss it with their neighbors, then ask for a volunteer to come and demonstrate it on the board. He will most likely demonstrate it correctly; laying your 1/3 strip end to end twice to find the 2/3 point.
If he doesn’t, or if the idea still seem counterintuitive to many of your students, go back to the idea of distance. Get a volunteer to come stand beside you and then walk three steps away. Ask him to come one third of the distance back (1 step). Then ask him to go back, and tell him now to come two thirds of the distance to you. Continue with other volunteers and other fractions until your students are comfortable with the idea.
Then transfer this idea onto your number line, and show how starting at zero and measuring two 1/3rds brings you to the 2/3 point on your number line.
Then have the children help you move tables and chairs to the back, so that you have a large empty space to work. If a gym or other large empty room is available, you may want to move there for the rest of this class. Otherwise, tailor the size of your number lines to match the available space.
Set up the number lines on the floor. Each number line will have four children manning it, so you’ll need to have as many number lines as the number of children in your class divided by four. These number lines will preferably be arranged side by side, in a line.
Assign the students to teams; four students to each number line. Give each student a strip of colored paper the size of one unit on their floor number lines. Then assign each student a fraction: in every group, you need a 1/3 student, a ¼ student, a 1/6 student, and a 1/8 student. Tape the designations on each student’s shirt. For a ‘handicapped race’ effect, give 1/3 and ¼ designations to the slower students, 1/6 and 1/8 designations to those that are faster. Each student will be called on the same number of times, but students with smaller fractions will have to do more counting and hopping.
Hand out the number strips and markers; in each group, one of each color. It helps organization if you give all students representing a particular fraction the same color.
If you have one odd student out, make him the caller. If you have two or three odd ones out, give them a number line and fractions.
Ask the students to mark where their fractions are on their number lines: 1/3, ¼, 1/6, and 1/8. They will do this with the strips of paper, folding them into appropriate sections as they did in yesterday’s lesson, and using those sections as rulers. Tell them to keep these strips of paper folded after they’ve used them. These strips are their ‘shoes’, and they’ll be needed again and again throughout the game.
Describe the game to them. The caller (you, if there wasn’t an extra student) stands at the front of the room with a pile of full-sized shuffled ‘hopscotch flashcards’. He picks one, displays it, and reads it out. Immediately the students representing that fraction take their ‘shoe’ – the paper strip—mark off the appropriate number of intervals, and then jump, once in each interval, to the fraction marker. For instance, if the caller picked “4/6” the 1/6 player would measure off 4 ‘1/6’ measures with his paper shoe, and then, as soon as they are measured, hop down to the fourth one, doing a one foot jump in each place. The first three to successfully measure and jump are awarded stickers on their fraction nametags: red for the first to hop to place, yellow for the second, and green for the third. Then they go back to the beginning, and the caller calls again.
They will soon discover that after they’ve been called once future calls are easier, as they will have marked off some (maybe all) of their fractions on the number line. Since they are using their colored markers, it will be easy to tell their intervals versus their team-mates. Before the game is halfway done, you should have no measuring at all; just quick, sure hopping when a new fraction is called.
Throughout the game, continue to interweave your class objectives with the game by asking at intervals, randomly, but of every student at least once: How far did you jump? (a steps) What was the size of the interval you jumped through (a/b)? Where is the point a/b on the number line (at the end of a 1/b steps).
Play as long as time permits; the game speeds up as you go, so you should be able to get through the stack of flashcards twice. At the end of the game the stars get tallied up on a per team basis: red is three points, yellow two points, green one point. The team with the greatest number of points wins.
Common Core Standards
This lesson plan is aligned to the Common Core Standard 3.NF.2. That item reads, in part:
3.NF.2. (b). Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line.
Web Resources/Further Exploration
This lesson plan gives you one fun way of making fractions come alive, but it’s best to approach every topic from multiple angles. That’s why I’m recommending Mathwarehouse’s wonderful fraction resources again— after all, they’re all free!
Common Core Standard 3.NF.2 Lesson Plans
Under 3.NF.2, third grade numbers and fractions item 2, the Common Core State Standards for Mathematics reads:
3.NF.2: Understand a fraction as a number on the number line; represent fractions on a number line diagram.
a. Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line.
b. Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line.
Lesson Plans on this Topic:
3rd Grade Lesson Plan: Fractions on the Number Line
Discussion/Introduction
Up to this point fractions have simply been discrete portions of tangible wholes; real parts that can be felt, seen, and tested. This third grade lesson plan, though, marks a water shed: we get to transfer our knowledge of ‘half a cookie’ to the more abstract concept of half a unit on a number line.
Objective
That students would be able to represent a fraction 1/b on a number line by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts, and that they’d understand that each part has size 1/b . Also, that they would understand that the endpoint of the part based at 0 locates the number 1/b on the number line.
Supplies
- Number line experiment worksheet for each student (download here)
- Precut (colored) strips of paper, ½-1 inch thick and the length of zero to one on the student’s number lines, and a few longer strips of paper for you to use with the number line you will draw on the blackboard
- Apple or other similar easily dividable item
Methodology/Procedure
Tell your students that they’ve become so good at identifying and dealing with fractions—portions of pie, pizza, or apples and oranges—that today they can take what they’ve learned to a whole new sphere.
Pick up an apple. Tell them that it is an apple; you can feel it, you can measure it with a ruler, and you can divide it into two equal parts with a sharp knife. Remind them you can do the same with pizza, and with almost any physical object, provided your knife is sharp enough.
Then ask them if there are other things they could divide in half, things they can’t touch, feel, or cut with a sharp knife.
Write a list of ideas on the blackboard. Some ideas might be groups of things (or people), air, water, time, or space.
Validate each addition to the list as you write it down, and then tell them that today you’re going to look at fractions of three special things: portions of time, space, and mathematical units.
Talk about time first. Ask what it means when we say ‘half an hour’, and get as many versions of the answer as possible. If no-one suggests it, tell them that one way of thinking about it is as half the distance from one hour to the other.
Draw a diagram of your day on the blackboard; essentially, a number line that describes your day. At this point, though, don’t describe it as a ‘number line’ to your students. Put sitting up in bed, the first thing you do in the morning, away on the far left side of your diagram. Put going to sleep as the last thing, and in the middle put lunch.
Tell your students that the area between waking up and lunch is your morning; and then shade the first half, and tell them it is half your morning. If the morning was four hours long, from eight to twelve, and you were feeling miserable half the morning, ask them how long you were feeling miserable. (2 hours) How long were you feeling okay? (Also 2)
Observe that if you look at time in that way, time is very similar to distance. Talk about the distance between the bed and the lunch table in your drawing, and what half of it means. Talk about half of the way from the place you are standing to the window. Walk four steps away from your desk, counting as you go, and ask how many steps it is to your desk. Ask how many steps you would need to walk if you wanted to walk only half the way back to the desk (2). What if you wanted to walk just a quarter of the way back? (1)
Now erase everything from the blackboard and draw a simple number line going from zero to three. Ask them what this is called (a number line). Remind them that since a number line is math, we can use it to mean anything. We get to use the same number line, in exactly the same way, whether we’re talking about cookies, pizza, time, or distance.
Tell them for now you’ll pretend it’s talking about pizza. Put your chalk at zero, write a small dot, and test the students on basic number line usage: Here, you see, I have no pizza. If I buy two pizzas—one peperoni and one sausage—where would I show that on the number line?
Your students should guide you to move your hand to the two. Do so, make a dot there, and then go back to the zero.
That was the day before yesterday, explain. Yesterday, I also started with no pizza. I also bought pizza. But I wasn’t feeling very hungry and didn’t have much spare money, so I only bought half. How can I show that on the number line? There isn’t any place that says ‘half’.
Listen to any ideas they come up to. If someone suggests dividing the portion of the number line between zero and one in two parts and making a dot on the middle line, tell him you really like that idea.
Take a strip of paper exactly as long as the distance between zero and one; fold it in half, lay it on the number line from 0 to ½, and draw your ‘half pizza’ dot. Shade the area on the line between 0 and ½. Ask your students how long that segment is; compared to the length between 0 and 1 (1/2 the length). Ask them where the segment starts (0).
Pick up the folded paper strip again, and ask how long it is (1/2 of what it used to be). Since it is ½, ask them if it means ½ wherever you place it on the number line—do you have to begin measuring off at zero, or can you start somewhere else instead? Get feedback as to why or why not before you explain that since ½ is just half of one, and you have no ‘wholes’ to add it to, you always have to start on zero when you measure its placement.
Ask them how you’d find out where to place a do for 1/4th. Fold your strip into fourths, and use the folded strip as a measuring stick to place a dot at exactly 1/4th.
Ask about 1/3, unfold your strip and refold into thirds, and prepare to make a 1/3 mark. Ask where you should start the strip when you measure off the 1/3 (at 0).
Ask which mark is closer to the zero (1/4); which is furthest away (1/2).
Then pass out the student worksheets and strips of paper. Your students will be marking ½, 1/3, ¼ and 1/6 on their own number lines. If you have not introduced 1/6th previously, you may need to walk your student through that fraction by marking your own 1/6 on the blackboard.
Common Core Standards
Under 3.NF.2, the Common Core State Standards for Mathematics reads:
3.NF.2 Understand a fraction as a number on the number line; represent fractions on a number line diagram.
- Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line.
Web Resources/Further Exploration
Here are some links to helpful web resources that might help your students learn to enjoy fractions. When they’ve decided that fractions are definitely fun, it’ll be easy to gain the familiarity and intuitive understanding they need to make a success of classroom work.
Common Core Standard 8.EE.A.1 Lesson Plans
In (8.EE.A.1), the Common Core State Standards for Mathematics reads ‘Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 32 × 3-5 = 3-3 = 1/33 = 1/27.’