|
Calculate Compound Interest
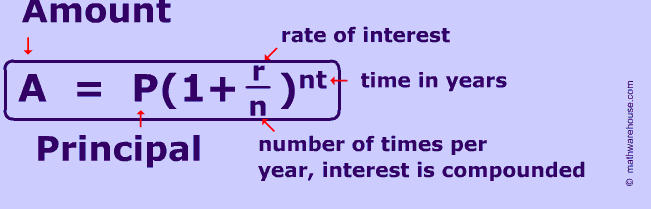
Formula for Compound Interest
To calculate compound interest use the formula below. In the formula, A represents the amount in the account
Practice Problems
Problem 1) If you have a bank account whose principal = $1000, and your bank compounds the interest twice a year at an interest rate of 5%, how much money do you have in your account at the year's end?
Problem 2) If you start a bank account with $10,000 and your bank compounds the interest quarterly at an interest rate of 8%, how much money do you have at the year’s end ? (assume that you do not add or withdraw any money from the account)
Problem 3)
The first credit card that you got charges 12.49 % interest to its customers and compounds that interest monthly. Within one day of getting your first credit card, you max out the credit limit by spending $1,200.00 . If you do not buy anything else on the card and you do not make any payments, how much money would you owe the company after 6 months?
| Final amount after compounding |
Note : since the duration of time is half of a year, the value of t in the is ½ . 6 months is half of a year, and t in the compound interest formula is measured in years
Top
|
