Quick Overview
If $$x$$ is approaching one of the transition points of the function, then you have to check both one-sided limits.
Examples
Example 1
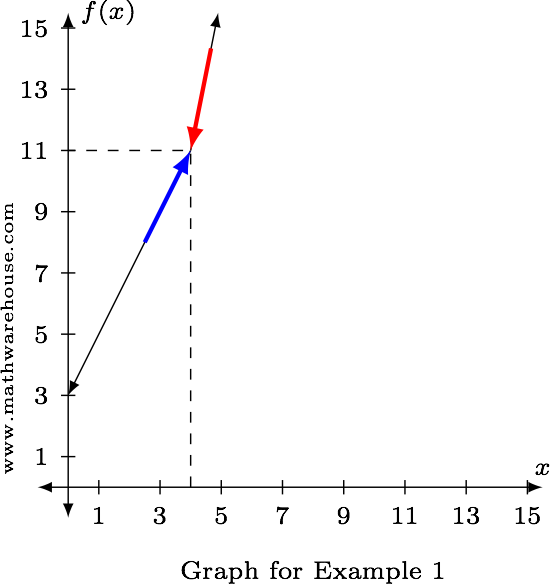
Determine $$\displaystyle\lim\limits_{x\to4} f(x)$$, if $$f$$ is defined as below.
$$ f(x) = \left\{% \begin{array}{ll} 2x+3, & x < 4\\ 5x - 9, & x \geq 4 \end{array} \right. $$
Evaluate the one-sided limits.
$$ \begin{align*} \lim_{x\to4^-} f(x) & = \lim_{x\to4^-} (2x+3) = 2(4)+3 = 11\\ & \\ \lim_{x\to4^+}f(x) & = \lim_{x\to4^+}(5x-9) = 5(4)-9 = 11 \end{align*} $$
If the one-sided limits are the same, the limit exists.
Answer: $$\displaystyle\lim\limits_{x\to4}f(x) = 11$$ when $$f$$ is defined as above.
Example 2
Evaluate $$\displaystyle\lim\limits_{x\to0} f(x)$$ when $$f$$ is defined as follows.
$$ \\ f(x) = \left\{% \begin{array}{ll} x^2+4,& x<0\\ \sqrt x,& x\geq 0 \end{array} \right. \\ $$
Examine the one-sided limits.
$$ \begin{align*} \lim_{x\to 0^-} f(x) & = \lim_{x\to 0^-}\,(x^2 +4) = (0)^2+4 = 4\\ & \\ \lim_{x\to0^+} f(x) & =\lim_{x\to0^+}\sqrt x = \sqrt 0 = 0 \end{align*} $$
If the one-sided limits are different, the limit doesn't exist.
Answer: $$\displaystyle\lim\limits_{x\to0} f(x)$$ doesn't exist when $$f$$ is defined as above.

Example 3
Suppose $$f$$ is defined as below. Determine the value of $$b$$ so that $$\displaystyle\lim\limits_{x\to5} f(x)$$ exists.
$$ \\ f(x) = \left\{% \begin{array}{ll} 2x-3,& x<5\\[6pt] \frac 2 3 x + b, & x \geq 5 \end{array} \right. \\ $$
Evaluate both one-sided limits.
$$ \begin{align*}% \lim_{x\to5^-} f(x) & = \lim_{x\to5^-}(2x-3) = 2(5)-3 = 7\\ \\ \lim_{x\to5^+} f(x) & = \lim_{x\to5^+}\left(\frac 2 3 x + b\right) = \frac{2(5)} 3 + b = \frac{10} 3 + b \end{align*} $$
Set the two limits equal to each other and solve.
$$ \\ \begin{align*} \frac{10} 3 + b & = 7\\[6pt] b & = 7 - \frac{10} 3\\[6pt] b & = \frac{11} 3 \end{align*} \\ $$
Answer: $$b = \frac{11} 3$$
Practice Problems
Examine the one-sided limits.
$$ \begin{align*} \lim_{x\to2^-} f(x) & = \lim_{x\to2^-} \left(\frac 3 2 x + 7\right) = \frac 3 2 (2) + 7 = 3 + 7 = 10\\ & \\ \lim_{x\to2^+} f(x) & = \lim_{x\to2^+} \left(3x+4\right) = 3(2)+4 = 10 \end{align*} $$
If the one-sided limits are the same, the limit exists.
Answer: $$\displaystyle\lim\limits_{x\to2} f(x) = 10$$ when $$f$$ is defined as above.
Examine both one-sided limits.
$$ \begin{align*}% \lim_{x\to4^-} f(x) & = \lim_{x\to4^-} \sin\left(\frac\pi 8 x\right) = \sin\left(\frac{4\pi} 8\right) = \sin\left(\frac\pi 2\right) = 1\\ & \\ \lim_{x\to4^+} f(x) & = \lim_{x\to4^+} \frac 1 4 x = \frac 4 4 = 1 \end{align*} $$
If the one-sided limits agree, the limit exists..
Answer: $$\displaystyle \lim_{x\to 4} f(x) = 1$$ when $$f$$ is defined as above
Examine both one-sided limits.
$$ \begin{align*}% \lim_{x\to1^-} f(x) & = \lim_{x\to1^-} (x-2)^2 = (1-2)^2 = 1\\ & \\ \lim_{x\to1^+} f(x) & = \lim_{x\to1^+}\frac 1 {x-1} = \frac 1 0\qquad\mbox{Division by zero!} \end{align*} $$
If one of the one-sided limits doesn't exist, the limit doesn't exist.
Answer: $$\displaystyle \lim_{x\to1} f(x)$$ does not exist when $$f$$ is defined as above.
Examine the one-sided limits.
$$ \begin{align*}% \lim_{x\to-5^-} f(x) & = \lim_{x\to-5^-} \left(\frac 3 5 x+ 2)\right) = \frac{3(5)} 5 + 2 = 5\\ & \\ \lim_{x\to-5^+} f(x) & = \lim_{x\to-5^+}\left(2x +\frac 8 3\right) = 2(-5) + \frac 8 3 = -\frac{22} 3 \end{align*} $$
If the one-sided limits don't agree, the limit does not exist.
Answer: $$\displaystyle \lim_{x\to-5} f(x)$$ does not exist when $$f$$ is defined as above.
Evaluate both one-sided limits.
$$ \begin{align*}% \lim_{x\to-6^-} f(x) & = \lim_{x\to-6^-} (x^2 +b) = (-6)^2+b = 36 + b\\ & \\ \lim_{x\to-6^+} f(x) & = \lim_{x\to-6^+}\left(\frac 1 2 x+9\right) = \frac{-6} 2 + 9 = -3 + 9 = 6 \end{align*} $$
Set the two one-side limits equal to each other, and solve.
$$ \begin{align*} 36 + b & = 6\\ b & = -30 \end{align*} $$
Answer: $$b = -30$$
Evaluate both one-sided limits
$$ \begin{align*}% \lim_{x\to3^-} f(x) & = \lim_{x\to3^+} (2x+7) = 2(3)+7 = 13\\ \\ \lim_{x\to3^+} f(x) & = \lim_{x\to3^+} (mx-4) = 3m-4 \end{align*} $$
Equate the two limits and solve.
$$ \\ \begin{align*} 3m-4 & = 13\\[6pt] 3m & = 17\\[6pt] m & = \frac{17} 3 \end{align*} \\ $$
Answer: $$m = \frac{17} 3$$
Evaluate both one-sided limits.
$$ \begin{align*}% \lim_{x\to4^-} f(x) & = \lim_{x\to4^-} (mx+2b) = 4m + 2b\\ \\ \lim_{x\to4^+}f(x) & = \lim_{x\to4^+} (5x + b) = 20 + b \end{align*} $$
Since both limits must equal 10, set up the system of equations and solve.
$$ \\ \begin{align*} 4m + 2b & = 10\\ 20 + b & = 10\\[12pt] % 4m + 2b & = 10\\ b & = -10 && \mbox{Solve for \(b\) in the second equation.}\\[12pt] % 4m + 2(-10) & = 10 && \mbox{Substitute the value of \(b\) into the other equation.}\\ 4m - 20 & = 10\\ 4m & = 30\\[6pt] m & = \frac{30} 4\\[6pt] m & = \frac{15} 2 \end{align*} \\ $$
Answer: $$m = \frac{15} 2$$ and $$b = -10$$


















