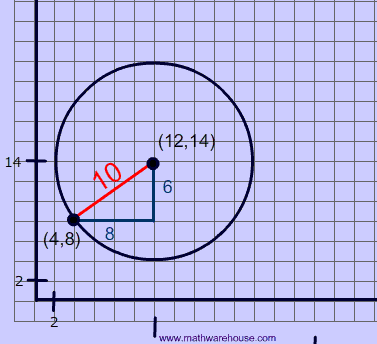
Distance Formula and Pythagorean Theorem
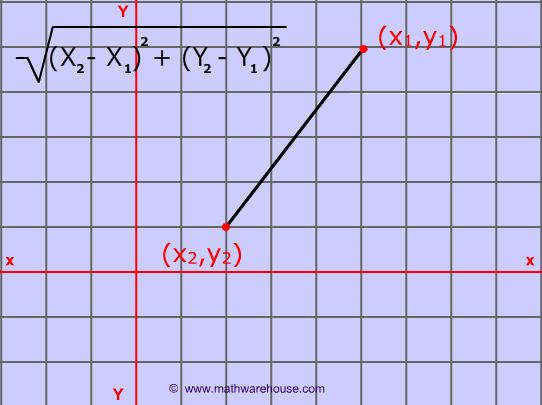
The distance formula is derived from the Pythagorean theorem. To find the distance between two points ($$x_1, y_1$$) and ($$x_2, y_2$$), all that you need to do is use the coordinates of these ordered pairs and apply the formula pictured below.
The distance formula is
$
\text{ Distance } = \sqrt{(x_2 -x_1)^2 + (y_2- y_1)^2}
$
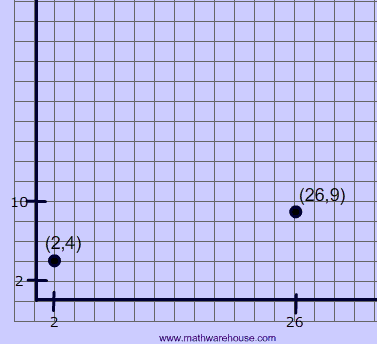
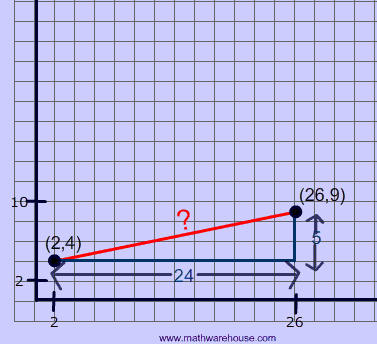
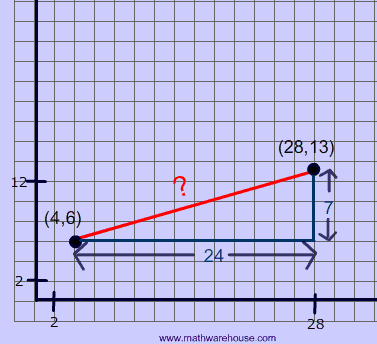
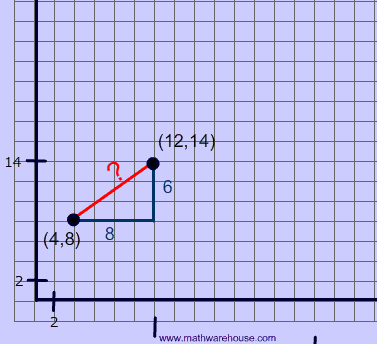
Below is a diagram of the distance formula applied to a picture of a line segment