In our previous post, we examined what binary numbers are, focusing primarily on what they look like. Now, let’s delve further into what it really means to be a binary number.
Before,we try to understand this, we need to make sure that you understand how ‘regular’ numbers work. Look at the math problem below. What is the sum of those numbers?
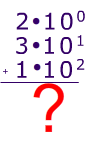
And as we all hopefully know, the sum is 132 as shown with the work below. (Remember your rules of exponents 100 is 1 (in fact, anything to the zero power is 1).
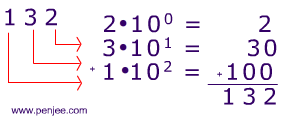
So, why am I showing you this?
Because, if you can think of 132 as a sum of powers of 10 (like below), then you will have no trouble understanding binary numbers.
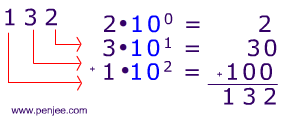
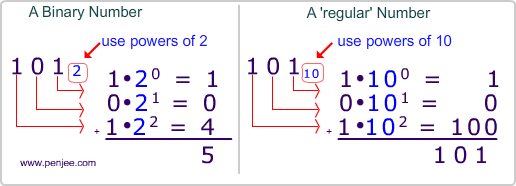
The main difference between ‘regular’ base 10 numbers and binary numbers is — binary uses powers of 2, instead of powers of 10. Let’s look at an example:

Here’s a side by side picture of a binary number like 1012 and regular number like 10110(“one hundred and one”).
Another example, can you figure out what 11012 means? In other words, what is 11012 as a ‘regular’ base 10 number?
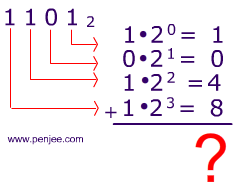
To get the answer to this problem, just add powers of 2 up (remember 20 = 1).
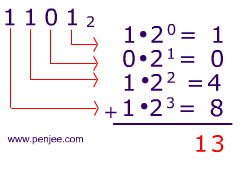
So, if we revisit our Binary Number Systems Joke, you should, hopefully, understand the humor:


