How to solve systems of 3 variable equations using elimination, step by step

Types of solutions
for systems of planes (3 variable equations)

What is a solution of system of equations with 3 variables?

Solution for system of lines

Just as the solution system of lines is where those lines meet, a solution for a system of 3 variable equations (planes), is again, just where these planes meet.

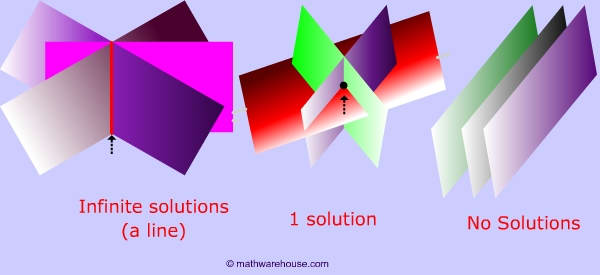
Why 3 planes?

If you want to solve a linear equation with 2 variables, you need 2 equations.

You can's solve $$ x + y = 1$$ , right? That's because you need equations to solve for 2 variables.

Similarly, if you have an equation with 3 variables, ( graphically represented by 3 planes), you're going to need 3 equations to solve it.

Two important terms

Consistent

Means that there is at least 1 intersection (solutions).

Inconsistent

Means that there are no intersections (solutions).

Ok, so how do we find that point of intersection?

Before attempting to solve systems of three variable equations using elimination, you should probably be comfortable solving 2 variable systems of linear equations using elimination.

Video Tutorial on using Elimination

Example 1

Example of how to solve a system of three variable equations using elimination.

Practice Problems

Problem 1

Use elimination to solve the following system of three variable equations.

A) 4x + 2y – 2z = 10
B) 2x + 8y + 4z = 32
C) 30x + 12y – 4z = 24

steps to solve 3 variable system by elimination

Problem 2

Use elimination to solve the following system of three variable equations.

A) x - y + z = -1
B) x + y + z = 3
C) 4x + 2y + z = 8

Problem 3

Use elimination to solve the following system of three variable equations.

A) 2x + 2y + 2z = -4
B) x + y + z = 3
C) 4x + 2y + z = 8

Although you can indeed solve 3 variable systems using elimination and substitution as shown on this page, you may have noticed that this method is quite tedious. The most efficient method is to use matrices or, of course, you can use this online system of equations solver. (all of our pictures on this topic)