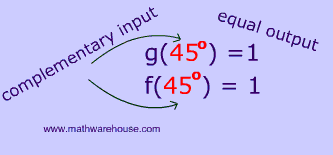Explore the pattern for
Cofunctions
Can you see a pattern below? Pay attention to the values of sine and cosine and their angle measurements.
| $$ \theta $$ | sin( $$ \theta $$ ) | $$ \theta $$ - 90 | cos($$ \theta $$- 90 ) |
| 10 ° | sin(10 ) = 0.17364817766693 | 90 - 10 = 80 ° | cos(80°) = 0.17364817766693 |
| 20 ° | sin(20 ) = 0.34202014332567 | 90 - 20 = 70 ° | cos(70°) = 0.34202014332567 |
| 30 ° | sin(30 ) = 0.5 | 90 - 30 = 60 ° | cos(60°) = 0.5 |
| 40 ° | sin(40 ) = 0.64278760968654 | 90 - 40 = 50 ° | cos(50°) = 0.64278760968654 |
| 50 ° | sin(50 ) = 0.76604444311898 | 90 - 50 = 40 ° | cos(40°) = 0.76604444311898 |
| 60 ° | sin(60 ) = 0.86602540378444 | 90 - 60 = 30 ° | cos(30°) = 0.86602540378444 |
| 70 ° | sin(70 ) = 0.93969262078591 | 90 - 70 = 20 ° | cos(20°) = 0.93969262078591 |
| 80 ° | sin(80 ) = 0.98480775301221 | 90 - 80 = 10 ° | cos(10°) = 0.98480775301221 |
| 90 ° | sin(90 ) = 1 | 90 - 90 = 0 ° | cos(0°) = 1 |
Sine Cosine
on a TI Calculator

So, did you notice the pattern?
So, what is a cofunction?

- Two functions whose complementary input angles $$ \rightarrow $$ evaluate to equal output
- It's important to note that the functions are not complementary
- Complementary input produces equal output.
![pair of cofunctions input output example]()
![pair of cofunctions input output example]()
So, what does that mean?

- In summary: Input is complementary and output is equal.
Most Common
Cofunction Formulas
sine and cosine
tangent and cotangent
secant and cosecant
Cofunctions Graphically
You can see the relationship between sine and cosine, graphically, when you plot $$ sin( \theta) $$ and $$ cos( \theta)$$ on the same set of axes
Concept Questions
![]() False.
False.
The functions themselves (sine and cosine) are not complementary . Being a cofunction, means that complementary input angles leads to the same output , as shown in the following example:

![]() True.
True.
Since the input angles are complementary and yield the same output, $$f(x)$$ and $$ g(x) $$ are cofunctions.

In this case, we can even figure out what the functions for $$ g(x)$$ and $$ f(x)$$ are :
$ g = sin \\ f= cos $ You can try for yourself, by entering the following values into your calculator: $ g( 60^{\circ}) = cos (60^{\circ} ) = .5 \\ f( 30^{\circ}) = sin (30^{\circ} ) = .5 $
Still need more convincing, here's a reminder of the animated gif showing a TI graphing calculator showing these very calculations:

Practice Problems
Since sine and cosine are cofunction, we know that the angles are complementary ; $ sin ( \red \theta ) = cos( \red{ 15^{\circ} } ) \\ \red \theta + \red{ 15^{\circ}} = 90 ^{\circ} \\ \red \theta = 90 ^{\circ} - 15^{\circ } \\ \theta = \boxed { 75^{\circ }} $
![]() False.
False.
The output of cofunctions is not complementary!!! We need complementary input to give us ( or evaluate to if you want to use technical math speak) equal output.
![]() True .
True .
Yes this solves the two requirements of cofunctions
- complementary input $$ \rightarrow$$ yields equal output
Thanks, to our cofunction formula, we know that $$ cos(80^{\circ}) = sin(10^{\circ}) $$
$$ 210^{\circ} $$ is in the third quadrant with a reference angle of $$ 30^{\circ} $$ .
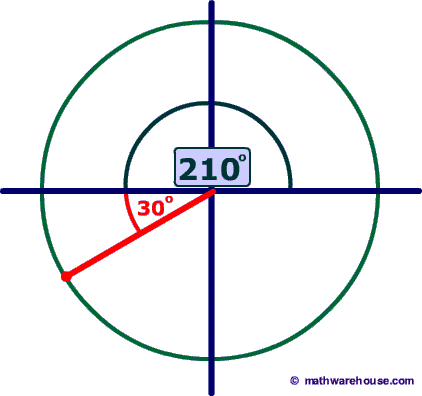
So, we know that $$ cos(210^{\circ}) = \red - cos(30^{\circ}) $$ To get an angle greater than $$ 45^{\circ}$$, we can use the cofunction of cosine: sine $ -cos(30^{\circ}) = - sin(60^{\circ} ) \\ \boxed{ - \sin( {\red{60^{\circ} }}) } $
$$ 265^{\circ} $$ is in the third quadrant with a reference angle of $$ 85^{\circ} $$ .
So, we know that $$ tan(265^{\circ}) = tan(85^{\circ}) $$ To get an angle less than $$ 45^{\circ}$$, we can use the cofunction of tangent : cotangent $ tan( \red{ 85^{\circ}}) = cot( \red{ 90-85^{\circ } }) \\ \boxed{ \cot( {\red{5^{\circ} }}) } $