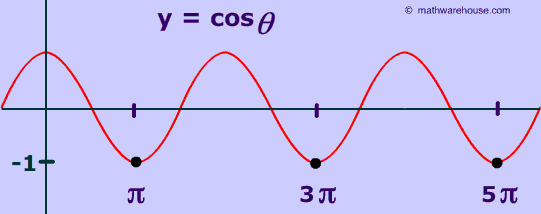
The inverse cos of 1, ie cos-1(1) is a very special value for the inverse cosine function. Remember that cos -1(x) will give you the angle whose cosine is x
The Value of the Inverse Cos of 1
As you can see below, the inverse cos-1 (1) is 0° or, in radian measure, 0 . '1' represents the maximum value of the cosine function. It happens at 0 and then again at 2Π, 4Π, 6Π etc..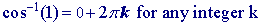 
(see second graph below.)
Below is a picture of the graph of cos(x) with over the domain of 0 ≤x ≤4Π with cos-1(1) indicted by the black dot. As you can see from the graph below, cosine has a value of -1 at 0 and again at 2Π and 4Π and every 2Π thereafter.
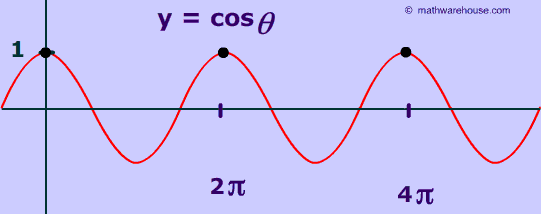
The Value of the Inverse Cos of -1
As you can see below, the cos-1 (1) is 270° or, in radian measure, 3Π/2 . '-1' represents the minimum value of the cosine function ever gets and happens at Π and then again at 3Π ,at 5Π etc.. 
(See graph at bottom )
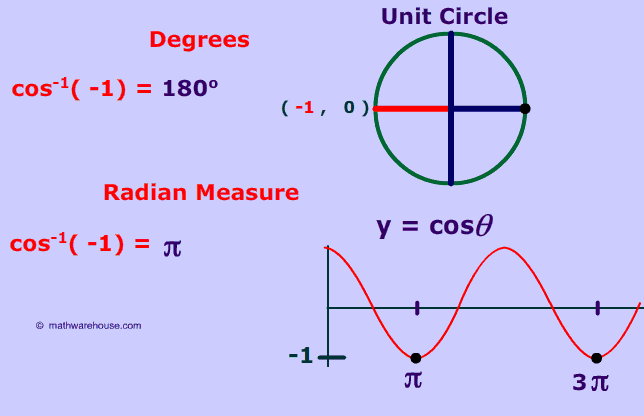
Below is a picture of the graph of cos(x) with over the domain of 0 ≤x ≤4Π with cos-1(-1) indicted by the black dot. 
