A regression is a process that takes all the points and calculates the equation that best 'fits' those points. A linear regression simply means that the equation will be the equation of a line. Although a linear regression can be quite helpful in understanding data, it can sometimes be misleading, as Anscombe's Quartet shows.
How to Calculate A Linear Regression
Examples of Linear Regressions and Graphs
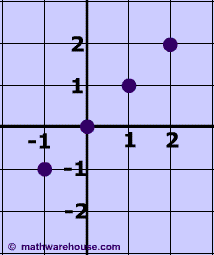
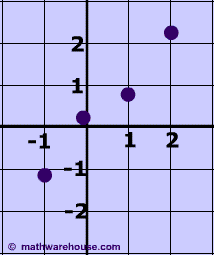
In both cases, the line of best fit is the y = x. As you can see from both graphs, this equation is a better fit for the first set of points but it still fits the 2nd set pretty well.
1st set of points
2nd Set of points
Practice Problems
The linear regression that best fits these points is the equation
y = ¼x +7.75
Now, using this equation what is the y value when x = 54?
Substitute x = 54 into the linear regression equation that you just found
y = ¼x + 7.5
y = ¼(54) + 7.5
y = 21
Problem 2
The accompanying table shows the enrollment of a preschool from 1980 through 2000. Write a linear regression equation to model the data in the table. Predict what the enrollment will be in the year 2010
The linear regression that best fits these points is the equation
y = 1.08x − 2125
Now, using this equation what is the y value when x = 2010?
Substitute x = 2010 into the linear regression equation that you just found
y = 1.08(x) − 2125
y = 1.08(2010) − 2125
y = 55
