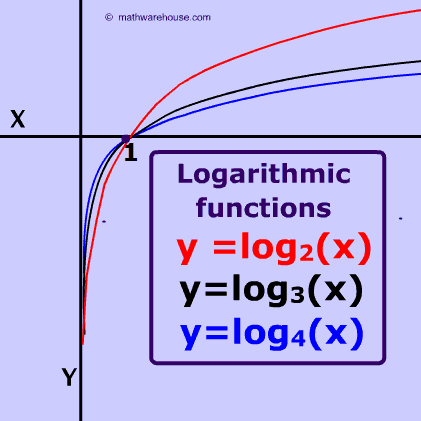
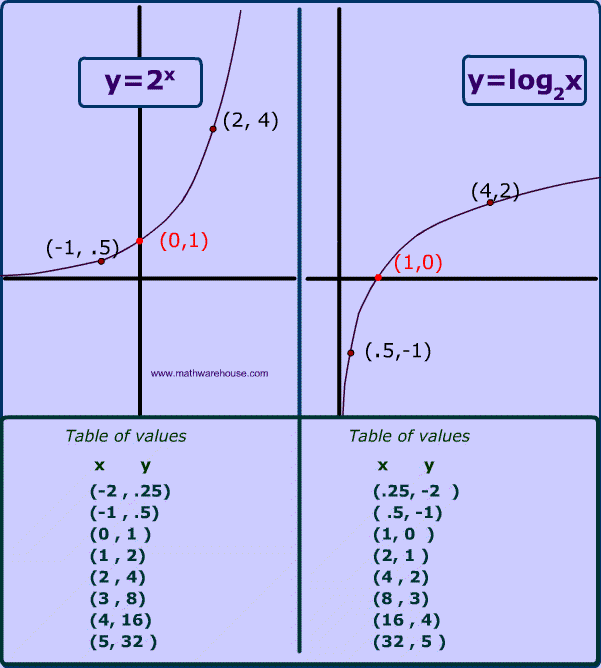
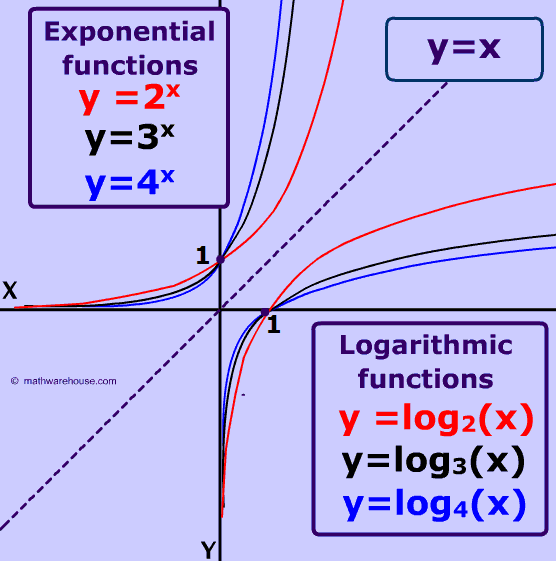
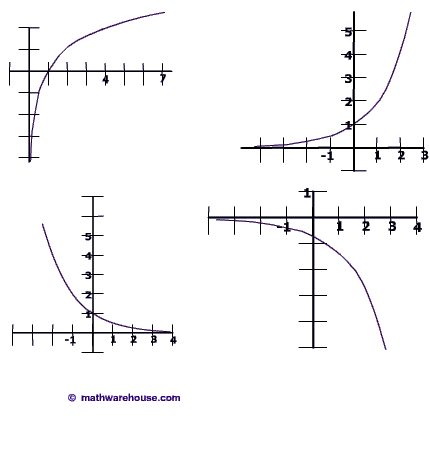
Graph of Logarithm: Properties, example, appearance, real world application, interactive applet

Logarithm Graph Applet
Explore graph, graph of inverse and its properties

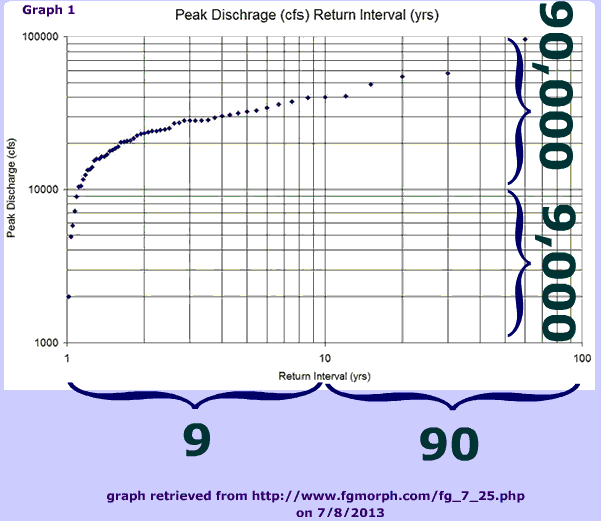
So what does a log graph look like?

There are two main 'shapes' that a logarithmic graph takes. Depending on whether b in the equation $$ y= log_b (x) $$ is less than 1 or greater than 1.

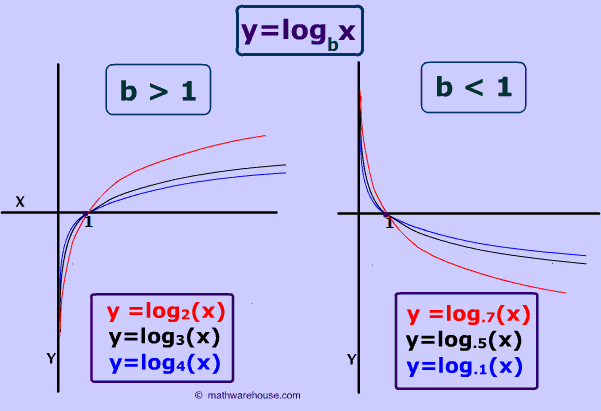
relationship between equation and graph of logarithm

Note: The two pictures up above do not include the case of b = 1.

Can you figure out why? What is special about the graph of $$ y = log_1 (x) $$?

Properties of Graph

Below you can see the graphs of 3 different logarithms. As you can tell, logarithmic graphs all have a similar shape.

Property 1

All logarithmic graphs pass through the point.

(1,0)

Property 2

The domain is:

All positive real numbers (not zero).

$$ \{x: x \in \mathbb{R}^+\} $$

Property 3

The range is: all real numbers.

$$ \{x: x \in \mathbb{R}\} $$

Property 4

It is a one-to-one function.

All real numbers. $$ \{x: x \in \mathbb{R}\} $$

Property 5

Has an asymptote that is a vertical line :

Property 6

Grow very slowly for large X ( explore with this applet ).

Property 7

Does not have horizontal asymptotes

Property 8

Based on the table of values below, exponential and logarithmic equations are:

Inverse functions!

Remember: Inverse functions have 'swapped' x,y pairs.

logarithms vs exponential function as inverses and table of values

Property 9

As the inverse of an exponential function, the graph of a logarithm is a reflection across the line y = x of its associated exponential equation's graph.

picture of logarithm graphs as inverses of exponential functions

Practice Problems

Problem 1

Can you identify which equation below represents a logarithmic equation?

Logarithmic graphs.

What are some applications of Logarithmic Graphs?

There are many real world examples of logarithmic relationships. Logarithms graphs are well suited.

When you are interested in quantifying relative change instead of absolute difference. Consider for instance the graph below.
When you want to compress large scale data. Consider for instance that the scale of the graph below ranges from 1,000 to 100,000 on the y-axis and 1 to 100 on the x-axis--such large scales which can be typical in scientific data are often more easily represented logarithmically.
pH scale for measuring acidity of a substance, decibel levels for audio measurement and the Richter scale for measuring earthquakes are all logarithmic. Read more at wikipedia about this.