-
Related Links:
- Triangles
- Triangle Types
- Interactive Triangle
- images
Definition
of the Incenter of a Triangle
The incenter is one of the triangle's points of concurrency formed by the intersection of the triangle's 3 angle bisectors.
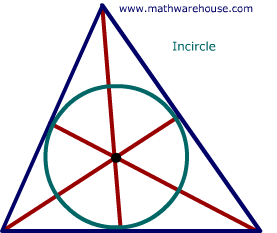
These three angle bisectors are always concurrent and always meet in the triangle's interior (unlike the orthocenter which may or may not intersect in the interior). The incenter is the center of the incircle . The incenter is the one point in the triangle whose distances to the sides are equal. (See picture)
- If the triangle is obtuse, such as the one on pictured below on the left, then the incenter is located in the triangle's interior.
- If the triangle is acute, then the incenter is also located in the triangle's interior.
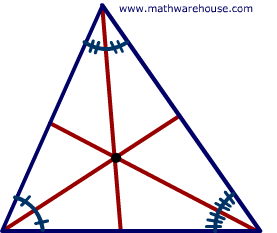

What about the incenter of a right triangle?
The illustrations above demonstrate that the incenter of an obtuse triangle and an acute triangle's is located in the interior. So the question is, where is the incenter located in a right triangle?

The incenter is always situated in the triangle's interior, regardless of the type of the triangle.
Incircle of a Triangle
The incircle of a triangle is the largest circle that fits in a triangle and its center is the incenter.. Its center is the one point inside the triangle that is equidistant from all sides of the triangle.(See first picture below)
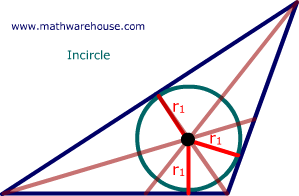
Diagram illustrating incircle as equidistant from each side
Pictures of the incircle