Find Height of Triangle given Area. Step by step tutorial with examples and pictures

Object of this page: To practice applying the conventional area of a triangle formula to find the height, given the triangle's area and a base.

Example

Example 1

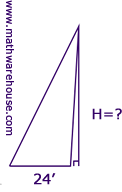
In diagram 1 , the area of the triangle is 17.7 square units, and its base is 4.

Directions: Calculate its height

Diagram 1

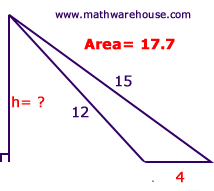
The red measurements are the ones that are relevant to this problem.

Diagram 2

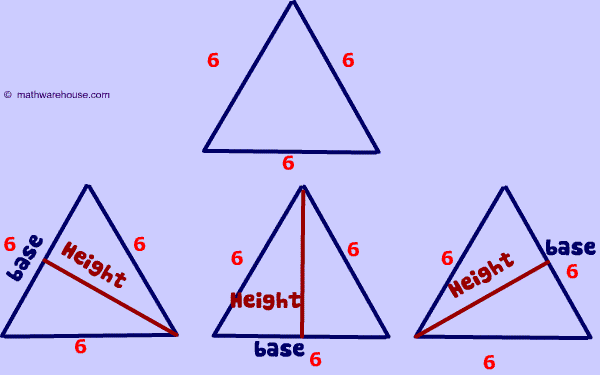
Remember that every triangle can have 3 base/height pairs. So, to solve this type of question, you must first identify the base..

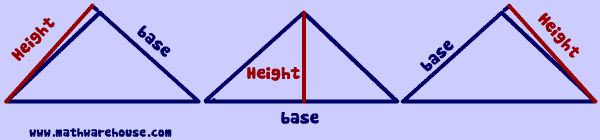So whenever you are talking about the height, we have to make sure we know which of the 3 'bases' (or sides) of the the triangle we are talking about.

Diagram 3

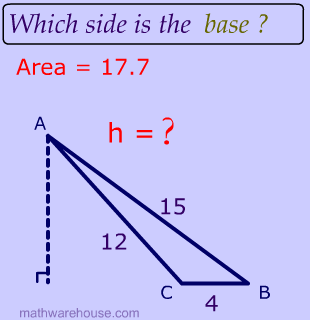
Remember: the height is perpendicular to the base , which is $$ \overline{CB}$$. And $$ \overline{CB} $$ has a measure of 4. We cannot use the other sides to help us solve this problem. So, for the rest of this lesson, your first task is to identify the which side is the base, especially when you get to the more challenging ones.

Steps :

Step 1

Substitute known values into the area formula.

$ A = \frac 1 2 \cdot \text { base } \cdot \red {\text { height } } \\ 17.7 = \frac 1 2 \cdot 4 \cdot \red h $

Step 2

Find the height by solving for $$\red h $$.

$ 17.7 = \frac 4 2 \cdot \red h \\ 17.7 = 2 \cdot \red h \\ \frac{17.7}{2} = \red h \\ \red h = 8.85 $

Practice Problems

Problem 1

If the area of this triangle is 658.8 square feet and its base is 24 inches, what is the height?

This problem is very similar to example 1.

Step 1

Substitute known values into the area formula.

$ A = \frac 1 2 \cdot \text{base } \cdot \text{height} \\ 658.8 = \frac 1 2 \cdot 24 \cdot \red{ \text{h}} $

Step 2

Find the height by solving for $$h$$.

$ 658.8 = 12 \cdot \red h \\ \frac{658.8}{12} = h \\ h = 54.9 $

Problems 2 and 3 ...(practice applying formula , no need to choose base side)

Problem 2

If the Area of this triangle is 11.6 square units and its base is 2, what is its height?

Step 1

Substitute known values into the area formula.

$ A = \frac 1 2 \cdot \text{base} \cdot \red{ \text{height } } \\ 11.6 = \frac 1 2 \cdot 2 \cdot \red{ \text{h } } $

Step 2

Solve for the height.

$ 11.6 = 1 \cdot \red h \\ h = 11.6 $

Problem 3

If the Area of this triangle is 17.7 square units and its base is 15, what is its height?

Step 1

Substitute known values into the formula.

$ A = \frac 1 2 \cdot \text{base} \cdot \red{ \text{height } } \\ 17.7 = \frac 1 2 \cdot \text{15} \cdot \red{ \text{ h } } \\ $

Step 2

Find the height by solving for $$h$$.

$ 17.7 = 7.5 \red h \\ \frac{17.7}{7.5} = h \\ h = 2.4 $

Problem 4

If the Area of the triangle on the left is 35.8 square units,find its height.

This problem is very similar to example 1. In every triangle, there is 3 base/height pairs, but you can tell from the picture that the base is the side of length 12. Remember that the base and height are perpendicular.

Step 1

Substitute known values into the formula.

$ A = \frac 1 2 \cdot \text{base} \cdot \red{ \text{height } } \\ 35.8 = \frac 1 2 \cdot \text{12 } \cdot \red{ \text{h } } $

Step 2

Find the height by solving for $$h$$.

$ 35.8 = 6h \\ \frac{35.8}{6} =h \\ h = 5.9 $

Problem 5

If the Area of the triangle on the left is 73.5 square units, find the height.

This problem is very similar to example 1. In every triangle, there is 3 base/height pairs, but you can tell from the picture that the base is the side of length 11. Remember that the base and height are perpendicular.

Step 1

Substitute known values into the formula.

$ A = \frac 1 2 \cdot \text{base} \cdot \red{ \text{height } } \\ 73.5 = \frac 1 2 \cdot 11 \cdot \red{ \text{h} } $

Step 2

Solve for the height.

$ 73.5 = 5.5 \red h \\ \frac{73.5}{5.5} = h \\ h = 13.4 $

Problem 6

If the Area of the triangle on the left is 141.9 square units, find its height.

This problem is very similar to example 1. In every triangle, there is 3 base/height pairs, but you can tell from the picture that the base is the side of length 21. Remember that the base and height are perpendicular.

Step 1

Substitute known values into the formula.

$ A = \frac 1 2 \cdot \text{base} \cdot \red{ \text{height } } \\ 141.9 = \frac 1 2 \cdot 21 \cdot \red{ \text{h } } $

Step 2

Solve.

$ 141.9 = 10.5 h \\ \frac{141.9}{10.5} = h \\ h = 13.5 $

Some Challenge problems

All right, now let's try some more challenging problems involving finding the height of a triangle. You should be comfortable with the properties of equilateral and isosceles triangle types before attempting the following questions.

Challenge Problem

If the perimeter of an equilateral triangle is 18 and its area is 15.6 square units, what is the measure of its height? Also, does it matter which side you choose as your base?

Since this is an equilateral triangle and we know its perimeter is 18, we can figure out that each side has a length of 6. (18 / 3 = 6). It does not matter which base we choose, since all 3 heights (or altitudes) in an equilateral triangle are congruent. From this point, it's just a matter of following the steps we have been using throughout this web page:

Step 1

Substitute known values into the formula.

Area = $$ \frac{1}{2} \cdot base \cdot height$$

15.6 = ½(6)(h)

Step 2

Solve for the height.

$$ 15.6 = 3h \\ \frac{15.6}{3} = h \\ h = 5.2 $$