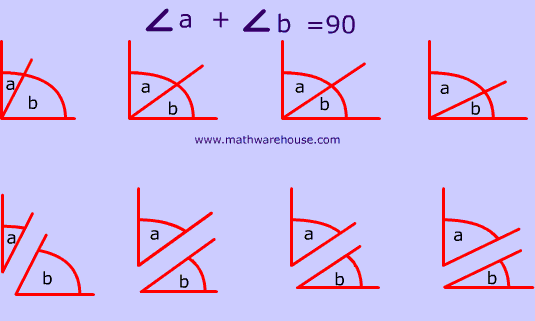Complementary Angles : Angles whose measure adds up to 90,but do they need to be next to each other?

What are complementary angles?

They are angles whose sum is 90°.

Do Complementary angles need to be next to
each other (ie adjacent)?

No!

Complementary angles do not need to be adjacent angles (angles next to one another).

All of the pairs of angles pictured below are complementary.

Practice Problems

Problem 1

What is the measure of $$ \angle a $$ below?

Since the angles are complementary (note: the perpendicular symbol).

$$ a + 50° = 90° \\ a = 90° -50° \\ a = 40° $$

Problem 2

What is the measure of $$ \angle a $$ below?

Since the angles are complementary (note: the perpendicular symbol).

$$ a + 57° = 90° \\ a = 90° - 57° \\ a = 33° $$

Problem 3

$$ \angle A $$ and $$\angle B$$ are complementary. If the $$m \angle A $$ is $$40^{\circ}$$, what is $$ m \angle B $$?

Since these angles are complementary we can set up the following equation.

$$ m\angle A + m\angle B = 90^{\circ} \\ $$

Now, substitute the known angle into equation and solve.

$$ 40^{\circ} + m\angle B = 90^{\circ} \\ 40^{\circ} \color{red}{- 40^{\circ}}+ m\angle B = 90^{\circ} \color{red}{- 40^{\circ}} \\ m\angle B = \color{red}{ 50^{\circ}} \\ $$

Problem 4

$$ \angle X $$ and $$\angle Z$$ are complementary. If the $$m \angle Z $$ is $$22^{\circ}$$, what is $$ m \angle X $$?

Since these angles are complementary we can set up the following equation:

$$ m\angle X + m\angle Z = 90^{\circ} \\ $$

Now, substitute the known angle into equation and solve.

$$ 22^{\circ} + m\angle X = 90^{\circ} \\ 22^{\circ} \color{red}{- 22^{\circ}}+ m\angle B = 90^{\circ} \color{red}{- 22^{\circ}} \\ m\angle B = \color{red}{ 68^{\circ}} \\ $$

Answer: 68 degrees.

Problem 5

If the ratio of two complementary angles is 2:1, what is the measure of the larger angle?

First, since this is a ratio problem, we know that 2x + 1x = 90, so now, let's first solve for x:

$$ 3x = 90 \\ x = \frac{90}{3} = 30 $$

Now, the larger angle is the 2x which is 2(30) = 60 degrees.

Answer: 60 degrees.

Problem 6

If the ratio of two complementary angles is 7:2, what is the measure of the smaller angle?

First, since this is a ratio problem, we know that 7x + 2x = 90, so now, let's first solve for x:

$$ 9x = 90 \\ x = \frac{90}{9} = 10 $$

Now, the smaller angle is the 2x which is 2(10) = 20 degrees.

Answer: 20 degrees.

Problem 7

If the measure of $$ \angle A = x^{\circ}$$, what is the measure of its complementary angle,$$ \angle B$$, in terms of x?

                                    $$
                                    m\angle A + m\angle B = 90
                                    \\
                                    x + m\angle B = 90
                                    $$
                                

                                Now, let's just solve for
                                
                                    $$
                                    \angle B
                                    $$
                                

                                    $$
                                    x + m\angle B = 90
                                    \\
                                    x \color{red}{- x} + m\angle B = 90\color{red}{- x}
                                    \\
                                    m\angle B = \color{red}{90 - x}
                                    $$
                                