What is Calculus

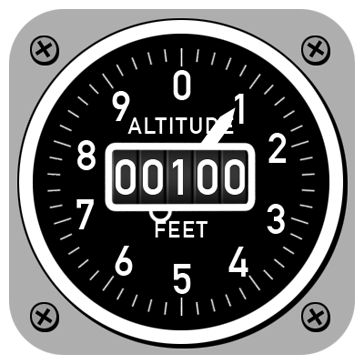Suppose you are enjoying a ride in a small airplane, and then you notice the altimeter reads only 100 feet above ground! Should you be worried?

Well...maybe. If the plane’s altitude is increasing, probably not.

On the other hand, what if the altimeter is showing 100 feet above ground, and your altitude is decreasing! Is that reason enough to worry?

Well...maybe. Even if the plane’s altitude is decreasing, perhaps it is sloo-o-wly descending. Perhaps the pilot is getting ready to land. No need to worry.

The point is, the plane's altitude alone isn’t enough information to determine whether or not there is a problem. But what does this have to do with calculus?

calculus is about measuring and describing change. In the scenario described above, knowing the plane's altitude at a particular moment in time, is equivalent to knowing a single point on the graph of a function

But that isn’t the whole story, is it? There’s the question of what comes next. Is the function going to increase? Or decrease? Even then, is the increase (or decrease) going to happen slowly? Or quickly? Will the function continue in this direction forever, or will it change direction? (See Figure 1)

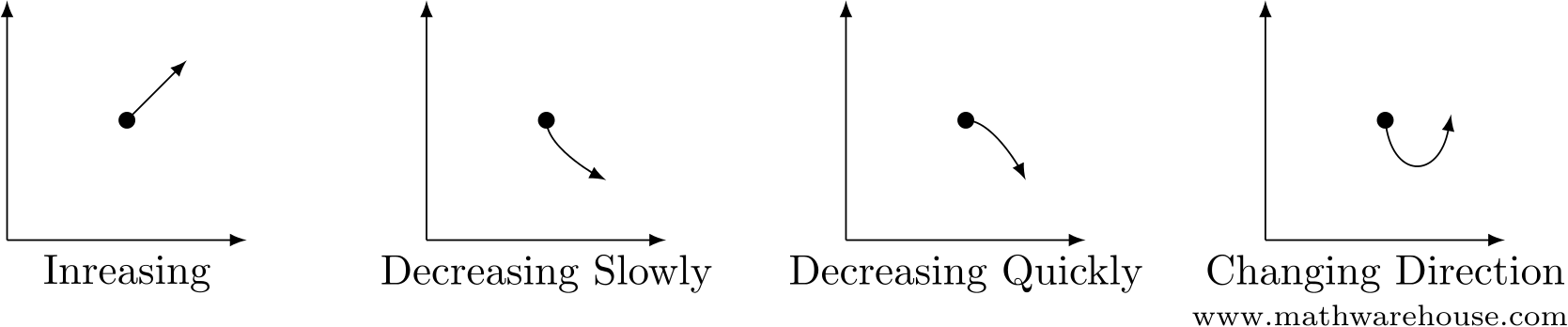
Figure 1: There’s more to the story than just function value. We care about direction, and how the function moves in that direction.

These questions cannot be handled by algebra alone. We need a more powerful set of tools, and those tools come bundled in a package called Calculus.

Calculus comes in two main parts.

• Differential Calculus: which is based on rates of change (slopes),
• Integral Calculus: which is based on adding up the effects of lots of small changes.

Additionally, each part of calculus has two main interpretations, one geometric and the other physical. (See below).

Let’s take a moment to look at each aspect of calculus.

Slopes

The slope of a line is well understood. It says that, no matter which two points you use, the ratio rise/run will always be the same.

But that’s not the case with a curve! (See Figure 2)

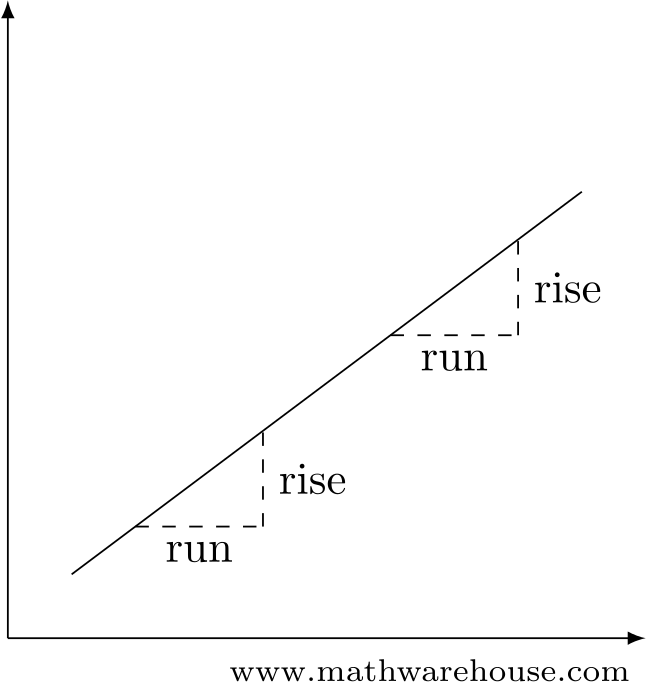
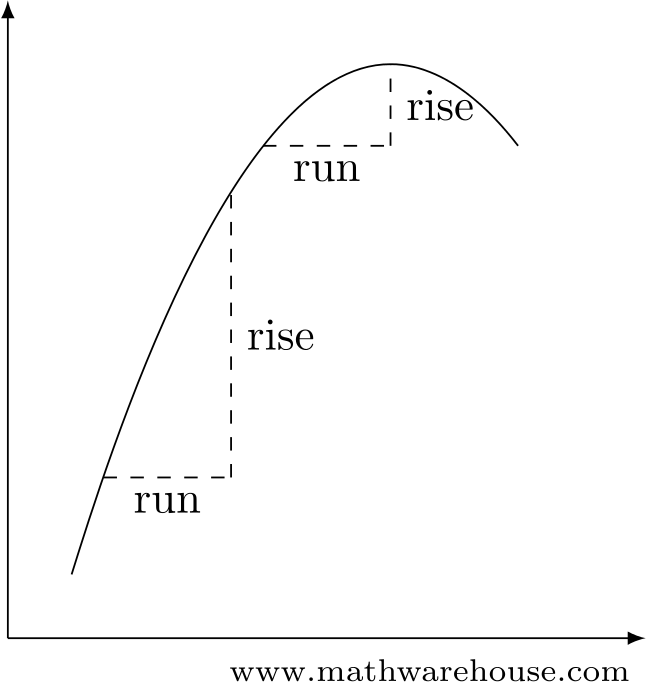
Figure 2: The rise/run ratio is the same everywhere for a line, but that’s not true for a curve

Slope of a Curve

We deal with this changing rise-to-run ratio on a curve by defining it at only one point at a time. To do that, we use the slope of the line that is tangent to the curve at that point (see Figure 3).

Differential calculus gives us the tools to find the slope of that tangent line.

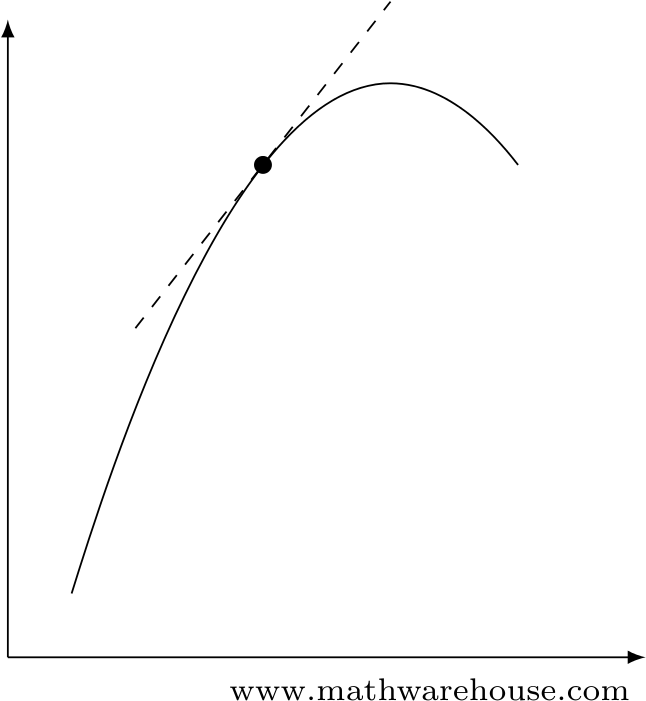
Figure 3: The slope of the line that is tangent to the curve gives us the slope of the curve at that point.

Velocities

For a physical understanding of Differential Calculus, think about traveling 120 miles in a car over a period of two hours, say from 1pm to 3pm.

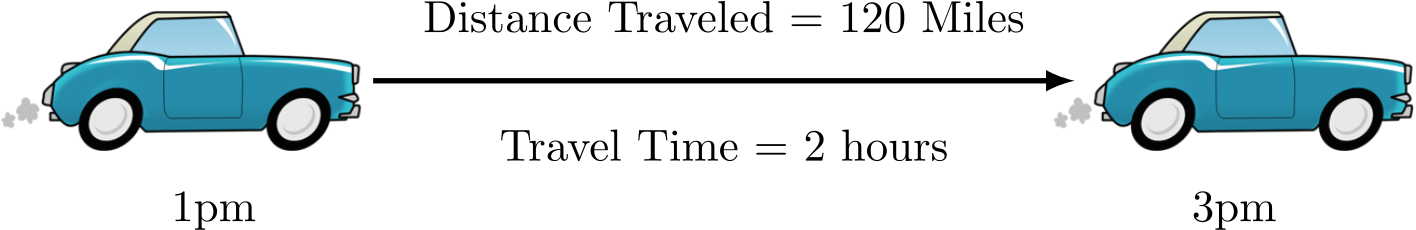
Well, 120 miles in 2 hours sounds like 60 miles per hour. Now, did you travel 60 miles per hour the entire time? Maybe. But you might have driven 65 miles per hour for a while, then had to slow down for a while (because of traffic) to only 50 miles per hour. Then perhaps you got to speed back up again. So we say that your average speed was 60 miles per hour for the trip.

But what was your exact speed at, say 2pm? Now, average speed is calculated as

$$\mbox{Average Speed} = \frac{\mbox{Change in Distance}}{\mbox{Change in Time}} = \frac{\mbox{(Final Position) - (Starting Position)}}{\mbox{(Final Time) - (Starting Time)}}$$

so we could figure out what our average speed was between 2:00 and 2:30,

• or between 2:00 and 2:15,
• or between 2:00 and 2:05,
• or between 2:00 and 2:01,
• or between 2:00 and 30 seconds later,
• or between 2:00 and 1 second later,
• or...

In each case, we can calculate a change in time and a change in position, but these are average speeds

How fast were you going at exactly 2:00? How do we calculate a speed at a single instant in time? There hasn’t been any change in time or any change in distance. And yet, you were traveling at 2:00, so you DID have a speed.

In order to answer this question, we need to have the tools of differential calculus.

Quick Summary: Both slopes and speeds are rates of change, and Differential Calculus is focused entirely on rates of change.

Areas

Finding the area of a rectangle is easy, its just $$A = (length)(width)$$.

Likewise, the area of a triangle is easy, its just $$A = \frac 1 2 (base)(height)$$.

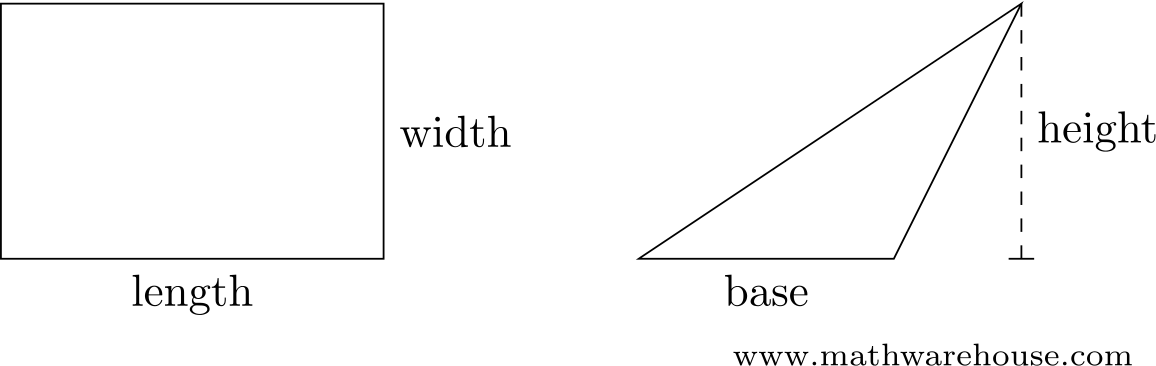
These two formulas allow us to calculate the area of figures that have straight edges, by dividing them into small triangles and rectangles:

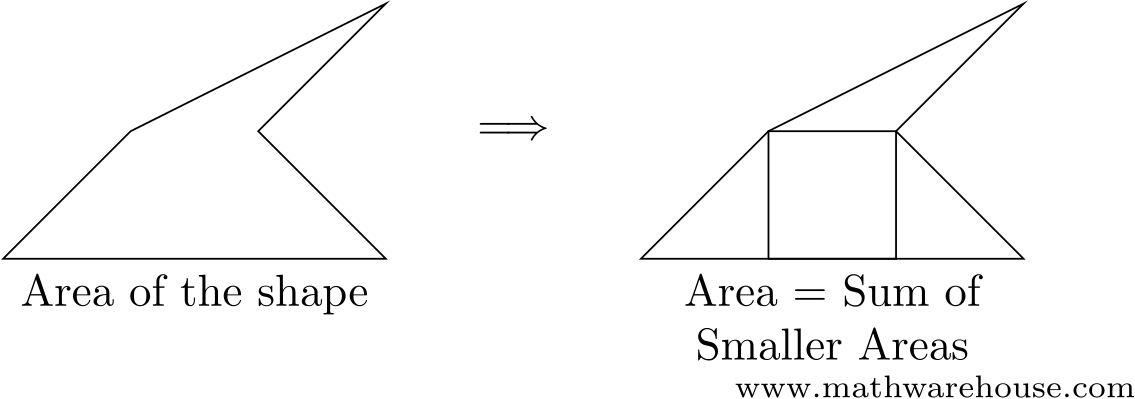
But if even one side of the figure is a curve...

suddenly calculating the area isn’t possible without the tools provided by integral calculus.

Net Change

Consider a dam holding back a huge volume of water. That water pushes against the dam face with a great deal of force.

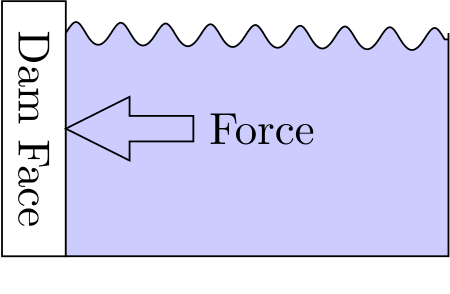
But the force isn’t the same everywhere on the face of the dam. The deepest parts of the water exert more force on the dam than the surface of the water.

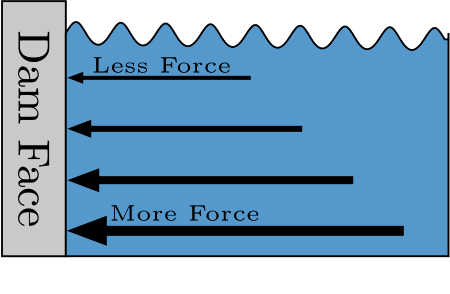
So, how much total force does the water exert on the dam face? Integral calculus gives us the tools we need to break the forces into very small¹ pieces that are easy to calculate, and then add them all up to give us the exact value of the total force!

Quick Summary: Integral Calculus calculates the effects of lots of small changes (like the changes in depth) and then adds all the effects together to give the total effect.

Both Differential and Integral Calculus are based on a single idea called “the limit.”

Figure 4: The function isn’t defined at $$x = 3$$.

For the function shown above, what is the $$y$$-value when $$x = 3$$? That is, what is the value of $$f(3)$$? The hole in the graph indicates that $$f(3)$$ is undefined, so there isn’t a function value for $$x = 3$$.

And yet, we can see by the graph that the function value would be 2 if we could somehow plug that hole in the graph. We can get around this “undefined” error by asking a slightly different question:

If $$x$$ is allowed to approach 3, getting closer and closer,² what value does $$y$$ approach?

¹Infinitesimally small!
²But not actually becoming equal to 3.

Whether we look at $$x$$-values to the left of 3, or to the right of 3, we can see that $$x$$-values that are closer to 3 are associated with $$y$$-values that are closer to 2.

This is known as finding the limit of the function, and it allows us to identify the location of that hole without getting an “undefined” error. (more here)

Quick Summary:

The limit of a function answers the question “Where is the $$y$$-value going as $$x$$ approaches this particular number?”

• Calculus is an area of math that deals with change.
• It has two main parts: Differential and Integral Calculus.
• Differential Calculus is based on rates of change (slopes and speed).
• Integral Calculus is based on accumulation of values (areas and accumulated change).
• Both parts of calculus are based on the concept of the limit.
• Both parts of calculus provide tools for answering questions that algebra alone cannot.