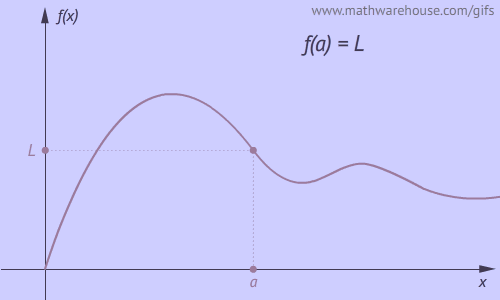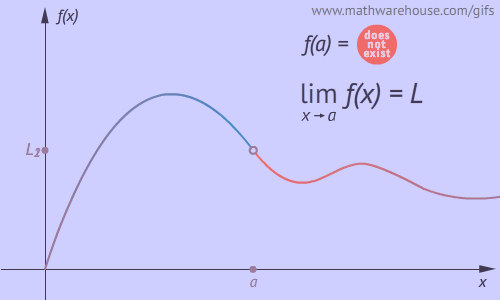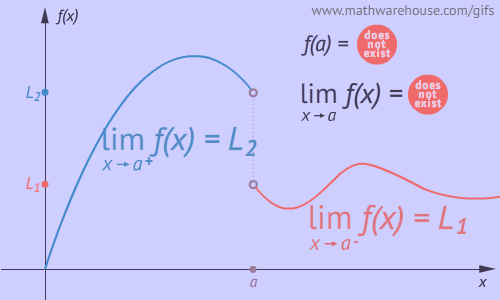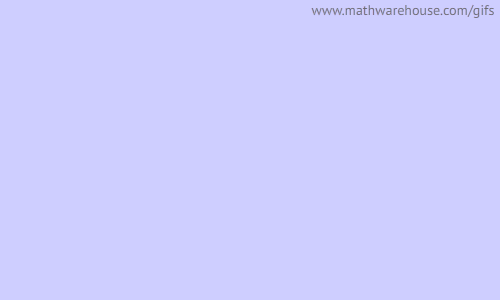
Quick Summary
Limits typically fail to exist for one of four reasons:
- The one-sided limits are not equal
- The function doesn't approach a finite value (see Basic Definition of Limit).
- The function doesn't approach a particular value (oscillation).
- The $$x$$-value is approaching the endpoint of a closed interval
Examples
Example 1: One-sided limits are not equal
Use the graph below to understand why $$\displaystyle\lim\limits_{x\to3} f(x)$$ does not exist.
$$f(x)$$ approaches two different values...
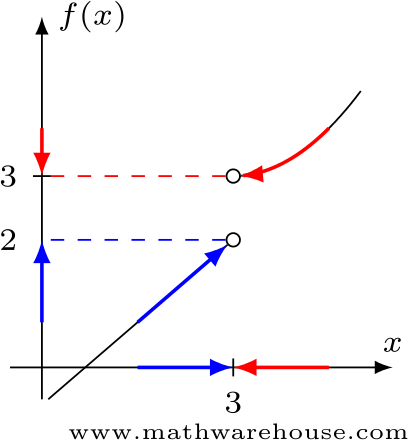
...depending on which direction $$x$$ approaches from.
In the graph, we notice that
$$\displaystyle\lim_{x\to3^-} f(x) \approx 2$$
and
$$\displaystyle\lim_{x\to3^+} f(x) \approx 3.$$
Even though the graph only allows us to approximate the one-sided limits, it is certain that the value $$f(x)$$ is approaching depends on the direction $$x$$ is coming from. Therefore, the limit does not exist.
Example 2: Infinitely Large Value
Use the graph below to understand why $$\displaystyle\lim\limits_{x\to 3} f(x)$$ does not exist.
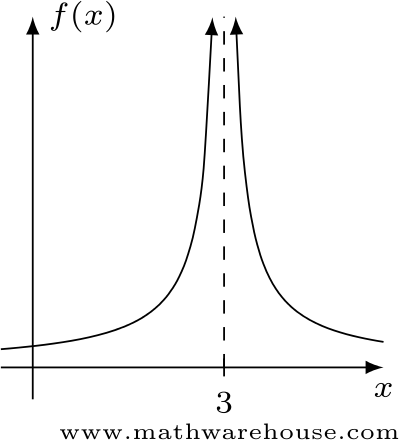
In order for a limit to exist, the function has to approach a particular value. In the case shown above, the arrows on the function indicate that the the function becomes infinitely large. Since the function doesn't approach a particular value, the limit does not exist.
Example 3: Infinite Oscillations
What is $$\displaystyle\lim\limits_{x\to0} \sin(\frac 1 x)$$?
Something interesting happens when you examine $$f(x) = \sin\left(\frac 1 x\right)$$ as $$x$$ approaches 0. The function begins to oscillate faster and faster.
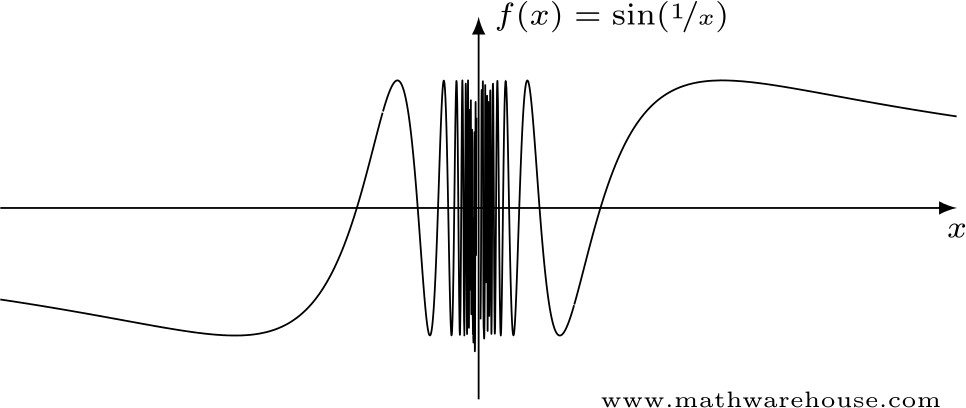
The closer $$x$$ gets to 0, the faster the function oscillates between 1 and -1. Is $$f(x)$$ approaching a single, particular value? No, it isn't. Consequently, the limit does not exist.
Example 4: End Points of an Interval
Examine $$\lim\limits_{x\to0} \sqrt x$$
Consider the graph of $$f(x) = \sqrt x$$ below. How would we determine the limit as $$x$$ approaches 0?

Since this function is only defined for $$x$$-values to the right of 0, we can't let $$x$$ approach from the left.
In order to say the limit exists, the function has to approach the same value regardless of which direction $$x$$ comes from (We have referred to this as direction independence). Since that isn't true for this function as $$x$$ approaches 0, the limit does not exist.
In cases like thi, we might consider using one-sided limits.