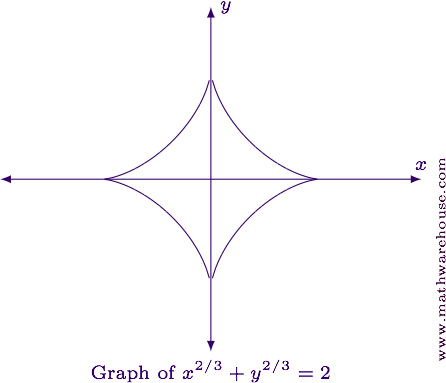
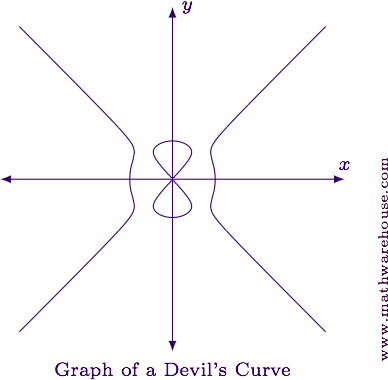
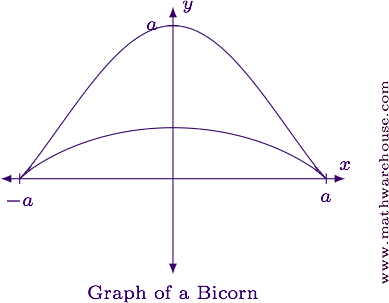
For reference, the graph of the equation is shown below.
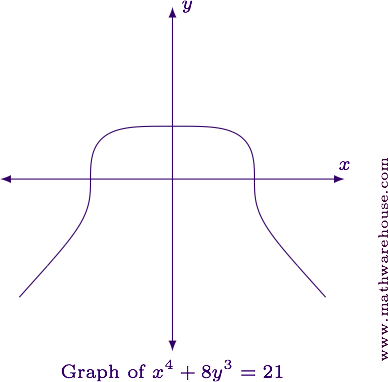
Differentiate the equation implicitly.
$$ \begin{align*} 4x^3 + 24y^2\cdot \frac{dy}{dx} & = 0 \end{align*} $$
Solve the equation for $$\frac{dy}{dx}$$
$$ \begin{align*} 4x^3 + 24y^2\cdot \frac{dy}{dx} & = 0\\[6pt] 24y^2\cdot \frac{dy}{dx} & = -4x^3\\[6pt] \frac{dy}{dx} & = - \frac{4x^3}{24y^2}\\[6pt] \frac{dy}{dx} & = - \frac{x^3}{6y^2} \end{align*} $$
$$\displaystyle \frac{dy}{dx} = - \frac{x^3}{6y^2}$$
Problem 2
The curve (shown below) generated by $$x^{2/3} + y^{2/3} = 2$$ is called an astroid, or a tetracuspid. Find $$\displaystyle \frac{dy}{dx}$$.
Differentiate the equation implicitly.
$$ \begin{align*}% \frac 2 3 x^{-1/3} + \frac 2 3 y^{-1/3}\cdot \frac{dy}{dx} & = 0 \end{align*} $$
Solve the equation for $$\frac{dy}{dx}$$.
$$ \begin{align*} \frac 2 3 x^{-1/3} + \frac 2 3 y^{-1/3}\cdot \frac{dy}{dx} & = 0\\[6pt] \blue{\frac 3 2}\left(\frac 2 3 x^{-1/3} + \frac 2 3 y^{-1/3}\cdot \frac{dy}{dx}\right) & = 0\cdot\blue{\frac 3 2}\\[6pt] x^{-1/3} + y^{-1/3}\cdot \frac{dy}{dx} & = 0\\[6pt] y^{-1/3}\cdot \frac{dy}{dx} & = -x^{-1/3}\\[6pt] \frac{dy}{dx} & = -\frac{x^{-1/3}}{y^{-1/3}}\\[6pt] \frac{dy}{dx} & = -\frac{y^{1/3}}{x^{1/3}} \end{align*} $$
$$\displaystyle \frac{dy}{dx} = -\frac{y^{1/3}}{x^{1/3}}$$
For reference, the graph of the equation is shown below.
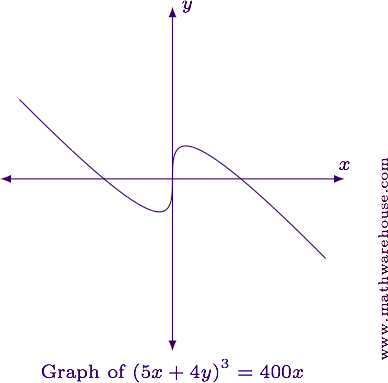
Differentiate implicitly.
$$ \begin{align*} 3\left(5x + 4y\right)^2\cdot\left(5 + 4\cdot\frac{dy}{dx}\right) & = 400 \end{align*} $$
Solve the equation for $$\frac{dy}{dx}$$.
$$ \begin{align*} 3\left(5x + 4y\right)^2\cdot\left(5 + 4\cdot\frac{dy}{dx}\right) & = 400\\[6pt] 5 + 4\cdot\frac{dy}{dx} & = \frac{400}{3\left(5x + 4y\right)^2}\\[6pt] 4\cdot\frac{dy}{dx} & = \frac{400}{3\left(5x + 4y\right)^2} - 5\\[6pt] \frac{dy}{dx} & = \frac{100}{3\left(5x + 4y\right)^2} - \frac 5 4 \end{align*} $$
$$\displaystyle \frac{dy}{dx} = \frac{100}{3\left(5x + 4y\right)^2} - \frac 5 4$$
For reference, the graph of the equation is shown below.
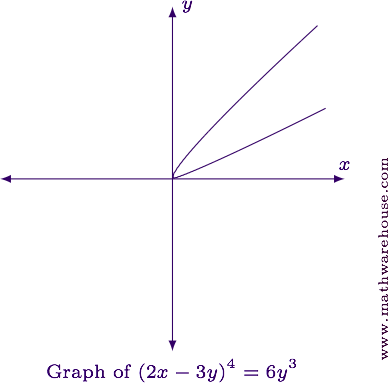
Differentiate the equation implicitly.
$$ \begin{align*} 4(2x-3y)^3\cdot\left(2 - 3\cdot \frac{dy}{dx}\right) & = 18y^2\cdot \frac{dy}{dx} \end{align*} $$
Distribute.
$$ \begin{align*} 8(2x-3y)^3 - 12(2x-3y)^3\cdot \frac{dy}{dx} & = 18y^2\cdot \frac{dy}{dx}\\[6pt] 4(2x-3y)^3 - 6(2x-3y)^3\cdot \frac{dy}{dx} & = 9y^2\cdot \frac{dy}{dx}\\[6pt] \end{align*} $$
Collect the $$\frac{dy}{dx}$$ terms on one side of the equation.
$$ \begin{align*} 4(2x-3y)^3 & = 9y^2\cdot \frac{dy}{dx} + 6(2x-3y)^3\cdot \frac{dy}{dx} \end{align*} $$
Factor out the $$\frac{dy}{dx}$$.
$$ \begin{align*} 4(2x-3y)^3 & = \left(9y^2 + 6(2x-3y)^3\right)\cdot \frac{dy}{dx} \end{align*} $$
Solve for $$\frac{dy}{dx}$$.
$$ \frac{dy}{dx} = \frac{4(2x-3y)^3}{9y^2 + 6(2x-3y)^3} $$
$$\displaystyle \frac{dy}{dx} = \frac{4(2x-3y)^3}{9y^2 + 6(2x-3y)^3}$$
For reference, the graph of the equation is shown below.
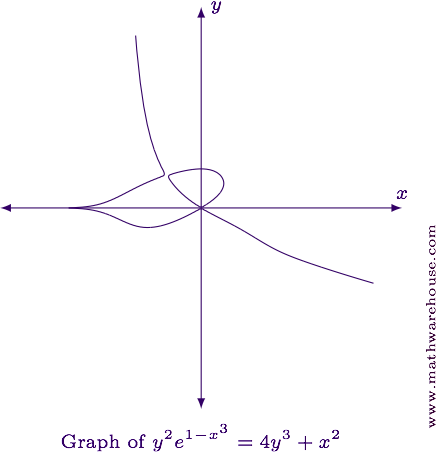
Differentiate the equation implicitly. Note that the left-hand side will require the the product rule.
$$ \begin{align*} 2y\cdot \frac{dy}{dx}\,e^{1-x^3} + y^2e^{1-x^3}(-3x^2) & = 12y^2\cdot \frac{dy}{dx} + 2x\\[6pt] 2y\cdot \frac{dy}{dx}\,e^{1-x^3} - 3x^2\,y^2e^{1-x^3} & = 12y^2\cdot \frac{dy}{dx} + 2x \end{align*} $$
Collect the $$\frac{dy}{dx}$$ terms on one side of the equation.
$$ \begin{align*} 2y\cdot \frac{dy}{dx}\,e^{1-x^3} - 3x^2\,y^2e^{1-x^3} & = 12y^2\cdot \frac{dy}{dx} + 2x\\[6pt] 2y\cdot \frac{dy}{dx}\,e^{1-x^3} - 12y^2\cdot \frac{dy}{dx} & = 2x + 3x^2\,y^2e^{1-x^3}\\[6pt] \end{align*} $$
Factor out the $$\frac{dy}{dx}$$.
$$ \begin{align*} 2y\cdot \frac{dy}{dx}\,e^{1-x^3} - 12y^2\cdot \frac{dy}{dx} & = 2x + 3x^2\,y^2e^{1-x^3}\\[6pt] \frac{dy}{dx}\left(2y\,e^{1-x^3} - 12y^2\right) & = 2x + 3x^2\,y^2e^{1-x^3} \end{align*} $$
Solve the equation for $$\frac{dy}{dx}$$.
$$ \begin{align*} \frac{dy}{dx} & = \frac{2x + 3x^2\,y^2e^{1-x^3}}{2y\,e^{1-x^3} - 12y^2} \end{align*} $$
$$ \displaystyle \frac{dy}{dx} = \frac{2x + 3x^2\,y^2e^{1-x^3}}{2y\,e^{1-x^3} - 12y^2} $$
For reference, the graph of the equation is shown below.
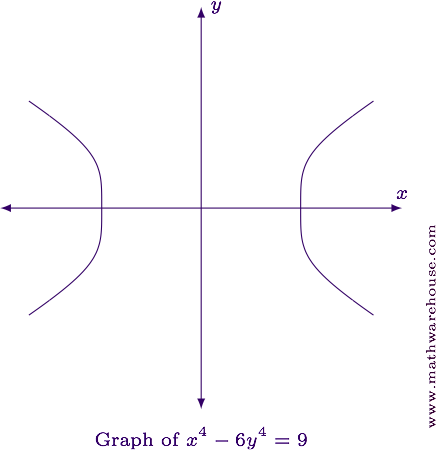
Differentiate implicitly.
$$ 4x^3 - 24y^3\cdot \frac{dy}{dx} = 0 $$
Solve for $$\frac{dy}{dx}$$.
$$ \begin{align*} 4x^3 - 24y^3\cdot \frac{dy}{dx} & = 0\\[6pt] - 24y^3\cdot \frac{dy}{dx} & = -4x^3\\[6pt] \frac{dy}{dx} & = \frac{-4x^3}{- 24y^3}\\[6pt] \frac{dy}{dx} & = \frac{x^3}{6y^3} \end{align*} $$
Differentiate implicitly again. Note that the right-hand side requires the quotient rule.
$$ \begin{align*} \frac{d^2y}{dx^2} & = \frac{6y^3\cdot 3x^2 - x^3\cdot 18y^2\cdot \frac{dy}{dx}}{(6y^3)^2}\\[6pt] & = \frac{18x^2y^3 - 18x^3y^2\cdot \frac{dy}{dx}}{36y^6}\\[6pt] & = \frac{18y^2\left(x^2y - x^3\cdot \frac{dy}{dx}\right)}{36y^6}\\[6pt] & = \frac{x^2y - x^3\cdot \frac{dy}{dx}}{2y^4} \end{align*} $$
Substitute in for $$\frac{dy}{dx}$$.
$$ \begin{align*} \frac{d^2y}{dx^2} & = \frac{x^2y - x^3\cdot \blue{\frac{dy}{dx}}}{2y^4}\\[6pt] & = \frac{x^2y - x^3\cdot \blue{\frac{x^3}{6y^3}}}{2y^4}\\[6pt] & = \frac{x^2y - \frac{x^6}{6y^3}}{2y^4}\\[6pt] & = \frac{\left(x^2y - \frac{x^6}{6y^3}\right)}{2y^4}\cdot \red{\frac{6y^3}{6y^3}}\\[6pt] & = \frac{6x^2y^4 - x^6}{12y^7} \end{align*} $$
$$\displaystyle \frac{d^2y}{dx^2} = \frac{6x^2y^4 - x^6}{12y^7}$$
For reference, the graph of the equation is shown below.
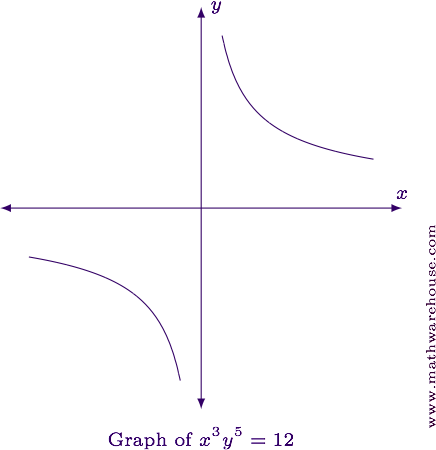
Differentiate implicitly.
$$ \begin{align*} 3x^2y^5 + x^3\cdot 5y^4\cdot \frac{dy}{dx} & = 0 \end{align*} $$
Solve for $$\frac{dy}{dx}$$.
$$ \begin{align*} 3x^2y^5 + x^3\cdot 5y^4\cdot \frac{dy}{dx} & = 0\\[6pt] 5x^3y^4\cdot \frac{dy}{dx} & = -3x^2y^5\\[6pt] \frac{dy}{dx} & = -\frac{3x^2y^5}{5x^3y^4}\\[6pt] & = -\frac{3y}{5x}\\[6pt] \end{align*} $$
Differentiate implicitly again.
$$ \begin{align*} \frac{d^2y}{dx^2} & = -\frac{(5x)\cdot 3 \cdot \frac{dy}{dx} - 3y\cdot 5}{(5x)^2}\\[6pt] & = -\frac{15x\cdot \frac{dy}{dx} - 15y}{25x^2}\\[6pt] & = -\frac{5\left(3x\cdot \frac{dy}{dx} - 3y\right)}{25x^2}\\[6pt] & = -\frac{3x\cdot \frac{dy}{dx} - 3y}{5x^2} \end{align*} $$
Replace $$\frac{dy}{dx}$$.
$$ \begin{align*} \frac{d^2y}{dx^2} & = -\frac{3x\cdot \blue{\frac{dy}{dx}} - 3y}{5x^2}\\[6pt] & = -\frac{3x\cdot \blue{\left(-\frac{3y}{5x}\right)} - 3y}{5x^2}\\[6pt]\\[6pt] & = -\frac{-\frac{9y} 5 - 3y}{5x^2}\\[6pt] & = -\frac{\left(-\frac{9y} 5 - 3y\right)}{5x^2}\cdot\red{\frac 5 5}\\[6pt] & = -\frac{-9y - 15y}{25x^2}\\[6pt] & = -\frac{-24y}{25x^2}\\[6pt] & = \frac{24y}{25x^2} \end{align*} $$
$$\displaystyle \frac{d^2y}{dx^2} = \frac{24y}{25x^2}$$
For reference, the graph of the equation is shown below.
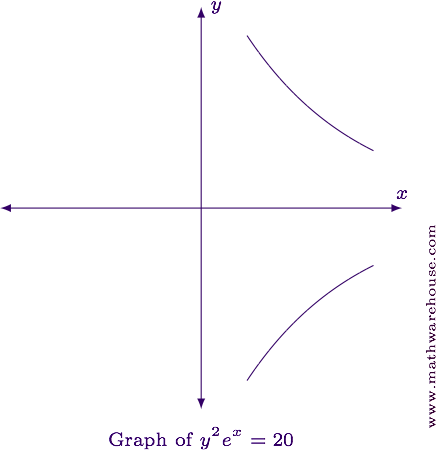
Differentiate implicitly using the the product rule.
$$ \begin{align*} 2y\cdot \frac{dy}{dx}\cdot e^x + y^2e^x & = 0 \end{align*} $$
Solve for $$\frac{dy}{dx}$$.
$$ \begin{align*} 2y\cdot \frac{dy}{dx}\cdot e^x + y^2e^x & = 0\\[6pt] 2y\cdot \frac{dy}{dx}\cdot e^x & = -y^2e^x\\[6pt] \frac{dy}{dx} & = -\frac{y^2e^x}{2ye^x}\\[6pt] & = -\frac 1 2 y \end{align*} $$
Differentiate implicitly.
$$ \frac{d^2y}{dx^2} = -\frac 1 2 \cdot \frac{dy}{dx} $$
Replace $$\frac{dy}{dx}$$.
$$ \frac{d^2y}{dx^2} = - \frac 1 2 \cdot \left(-\frac 1 2 y\right) = \frac 1 4 y $$
$$ \displaystyle \frac{d^2y}{dx^2} = \frac 1 4 y $$
Problem 9
The graph below shows an example of a type of curve called a Devil' Curve. The general equation for this type of curve is
$$ y^4 - x^4 + ay^2 + bx^2 = 0 $$
where $$a$$ and $$b$$ are constants. Find an expression for $$\frac{dy}{dx}$$.
Differentiate implicitly.
$$ \begin{align*} 4y^3\frac{dy}{dx} - 4x^3 + 2ay\frac{dy}{dx} + 2bx & = 0\\[6pt] 2y^3\frac{dy}{dx} - 2x^3 + ay\frac{dy}{dx} + bx & = 0 \end{align*} $$
Isolate the $$\frac{dy}{dx}$$ terms.
$$ \begin{align*} 2y^3\frac{dy}{dx} - 2x^3 + ay\frac{dy}{dx} + bx & = 0\\[6pt] 2y^3\frac{dy}{dx} + ay\frac{dy}{dx} & = 2x^3 - bx \end{align*} $$
Factor out the $$\frac{dy}{dx}$$.
$$ \begin{align*} 2y^3\frac{dy}{dx} + ay\frac{dy}{dx} & = 2x^3 - bx\\[6pt] \frac{dy}{dx}\left(2y^3 + ay\right) & = 2x^3 - bx \end{align*} $$
Solve for $$\frac{dy}{dx}$$.
$$ \begin{align*} \frac{dy}{dx}\left(2y^3 + ay\right) & = 2x^3 - bx\\[6pt] \frac{dy}{dx} & = \frac{2x^3 - bx}{2y^3 + ay} \end{align*} $$
$$ \displaystyle \frac{dy}{dx} = \frac{2x^3 - bx}{2y^3 + ay} $$
Problem 10
The graph below shows an implicit curve called a bicorn. The equation of the bicorn is
$$ y^2(a^2 - x^2) = (x^2 + 2ay - a^2)^2 $$
where $$a$$ is a constant. Find an expression for $$\frac{dy}{dx}$$.
Differentiate each side implicitly. Notice that the left-hand side will require the the product rule, while the right-hand side requires the chain rule. Also note that since $$a$$ is a constant, its derivative is 0.
$$ \begin{align*} 2y\frac{dy}{dx}(a^2 - x^2) + y^2(-2x) & = 2(x^2 + 2ay - a^2)\left(2x + 2a\frac{dy}{dx}\right)\\[6pt] 2y\frac{dy}{dx}(a^2 - x^2) -2xy^2 & = 4(x^2 + 2ay - a^2)\left(x + a\frac{dy}{dx}\right) \end{align*} $$
Distribute on the right-hand side.
$$ \begin{align*} 2y\frac{dy}{dx}(a^2 - x^2) -2xy^2 & = 4(x^2 + 2ay - a^2)\left(x + a\frac{dy}{dx}\right)\\[6pt] 2y\frac{dy}{dx}(a^2 - x^2) -2xy^2 & = 4x(x^2 + 2ay - a^2) + 4a(x^2 + 2ay - a^2)\frac{dy}{dx} \end{align*} $$
Collect all the $$\frac{dy}{dx}$$ terms on the left and the other terms on the right.
$$ \begin{align*} 2y\frac{dy}{dx}(a^2 - x^2) -2xy^2 & = 4x(x^2 + 2ay - a^2) + 4a(x^2 + 2ay - a^2)\frac{dy}{dx}\\[6pt] 2y\frac{dy}{dx}(a^2 - x^2) - 4a(x^2 + 2ay - a^2)\frac{dy}{dx} & = 4x(x^2 + 2ay - a^2) + 2xy^2 \end{align*} $$
Factor out the $$\frac{dy}{dx}$$.
$$ \begin{align*} 2y\frac{dy}{dx}(a^2 - x^2) - 4a(x^2 + 2ay - a^2)\frac{dy}{dx} & = 4x(x^2 + 2ay - a^2) + 2xy^2\\[6pt] \frac{dy}{dx}\left(2y(a^2 - x^2) - 4a(x^2 + 2ay - a^2)\right) & = 4x(x^2 + 2ay - a^2) + 2xy^2 \end{align*} $$
Solve for $$\frac{dy}{dx}$$.
$$ \begin{align*} \frac{dy}{dx}\left(2y(a^2 - x^2) - 4a(x^2 + 2ay - a^2)\right) & = 4x(x^2 + 2ay - a^2) + 2xy^2\\[6pt] \frac{dy}{dx} & = \frac{4x(x^2 + 2ay - a^2) + 2xy^2}{2y(a^2 - x^2) - 4a(x^2 + 2ay - a^2)} \end{align*} $$
$$ \displaystyle \frac{dy}{dx} = \frac{4x(x^2 + 2ay - a^2) + 2xy^2}{2y(a^2 - x^2) - 4a(x^2 + 2ay - a^2)} $$
