Quick Overview
- L'Hôpital is sometimes written L'Hospital.
- Regardless of how it is written, it is pronounced LO-pee-TAHL.
- L'Hôpital's Rule is used with indeterminate limits that have the form $$\frac 0 0$$ or $$\frac \infty \infty$$.
- L'Hôpital's Rule isn't a magic bullet. Sometimes it fails to find the value of a limit. But it does work a lot of the time.
- The basic idea of the rule is that
$$\displaystyle\lim_{x\to a} \frac{f(x)}{g(x)} = \displaystyle\lim_{x\to a} \frac{f'(x)}{g'(x)}$$
- L'Hôpital's Rule will also work for one-sided limits, and limits at infinity (when $$x\to\pm\infty$$).
- Sometimes you have to apply the rule more than once to get the answer.
Introduction
In earlier lessons (before we even had the derivative) we discussed different techniques for working with indeterminate limits . For example, we discussed limits such as
$$ \begin{array}{lcl} \lim\limits_{x\to-3}\,\frac{x^2+x-6}{x^2+8x+15} && \href{../limits/limits-indeterminate-factorable.php}{\text{The Factorable} \frac 0 0 \text{Form}}\\ % \lim\limits_{x\to \infty}\,\frac{3x + \sqrt{4x^2+5}}{6x+1} && \href{../limits/limits-at-infinity-roots-and-absolute-values.php}{\text{Limits At Infinity}}\\ % \lim\limits_{\theta\to0}\frac{\sin(a\theta)}{b\theta} && \href{../limits/limits-indeterminate-sine.php}{\text{Indeterminate Sine Forms}} \\ % \lim\limits_{x\to0}\,\frac{e^{ax}-1}{bx} && \href{../limits/limits-indeterminate-exponential.php}{\text{Indeterminate Exponential Forms}} \end{array} $$
among others. The above is not an exhaustive list of all the possible indeterminate forms. Unfortunately, many of those other indeterminate forms are not easily evaluated. At least, without the right tools.
Now that we have developed the idea of derivatives, however, we can use them as a tool for evaluating some of these more difficult indeterminate limits . This is accomplished using the technique known as L'Hôpital's Rule.
L'Hôpital's Rule (Basic Idea)
L'Hôpital's Rule tells us that derivatives and limits are related in the following way:
If $$\displaystyle \lim\limits_{x\to a} \frac{f(x)}{g(x)} = \frac 0 0\, \left(\mbox{or } \frac \infty \infty\right)$$, then we can use the derivative of $$f$$ and $$g$$ as follows:
$$ \displaystyle\lim_{x\to a} \frac{f(x)}{g(x)} = \displaystyle\lim_{x\to a} \frac{f'(x)}{g'(x)}.\longleftarrow \mbox{(Notice, these are the derivatives!)} $$
There are a couple of things to understand about L'Hôpital's Rule.
- The right-hand side of the equation is NOT the derivative of $$\frac{f(x)}{g(x)}$$, meaning it is not found by using the quotient rule. Instead, L'Hôpital's Rule treats the numerator and denominator as separate functions.
- Sometimes L'Hôpital's Rule has to be applied more than once in order to find the limit value.
- This rule is NOT a magic-bullet. There are some situations where the rule fails to produce a usable solution. That is, the limit remains indeterminate.
The proof that L'Hôpital's Rule is valid requires the use of Cauchy's Extension of the Mean Value Theorem (which we discussed in the previous lesson) and is included at the end of this lesson.
The proof is a good example of how the Mean Value Theorem can be used to prove other important ideas, but (to be honest) if you don't read or understand the proof of L'Hôpital's Rule, it won't hinder your ability to use it to evaluate limits. So, you can skip it if necessary (it is a really pretty proof, though. It's worth reading!).
Basic Applications of L'Hôpital's Rule
Example 1
Evaluate $$\lim\limits_{x\to0}\frac{\sin x} x$$.
Note that we have already learned about this particular limit. In an earlier lesson we showed that
$$ \displaystyle\lim_{x\to0}\frac{\sin x} x = 1. $$
The purpose of this example is to show that L'Hôpital's rule give us the same answer (which helps us believe the rule works, since we haven't proved it yet).
Step 1Show that the limit has the correct form for L'Hôpital's Rule $$\left(\frac 0 0\right.$$ or $$\left.\frac \infty \infty\right)$$.
$$ \displaystyle\lim_{x\to0}\frac{\sin x} x = \frac{\sin 0} 0 = \frac 0 0 $$
Step 2Use L'Hôpital's Rule, where $$f(x) = \sin x$$ and $$g(x) = x$$.
$$ \underbrace{\displaystyle\lim_{x\to0}\frac{\sin x} x = \displaystyle\lim_{x\to0} \frac{\blue{\frac d {dx}(\sin x)}}{\red{\frac d {dx} (x)}}}_{\mbox{L'Hôpital's Rule}} = \displaystyle\lim_{x\to0}\frac{\blue{\cos x}}{\red 1} = \frac{\cos 0} 1 = \frac 1 1 = 1 $$
Answer$$\lim\limits_{x\to0}\frac{\sin x} x = 1$$
For reference, here is a graph of the function near $$x = 0$$. Note that the function is undefined at $$x = 0$$.
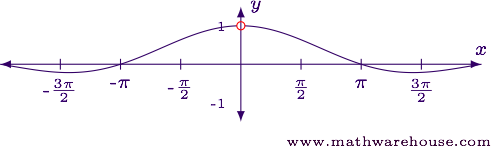
Example 2
Let's try one more that we could evaluate directly using techniques from an earlier lesson. This particular limit will require two applications of the rule.
$$ \mbox{Evaluate } \displaystyle\lim_{x\to\infty} \frac{3x^2 - 5x + 7}{4x^2 + 9x - 1}. $$
Step 1Verify the limit has the correct form for L'Hôpital's rule.
$$ \displaystyle\lim_{x\to\infty} \frac{3x^2 - 5x + 7}{4x^2 + 9x - 1} = \frac{\lim\limits_{x\to\infty}(3x^2 - 5x + 7)}{\lim\limits_{x\to\infty}(4x^2 + 9x - 1)} = \frac \infty \infty $$
Step 2Use L'Hôpital's Rule, where $$f(x) = 3x^2 - 5x + 7$$ and $$g(x) = 4x^2 + 9x - 1$$.
$$ \underbrace{\displaystyle\lim_{x\to\infty} \frac{3x^2 - 5x + 7}{4x^2 + 9x - 1} = \lim_{x\to\infty} \frac{\blue{\frac d {dx} (3x^2 - 5x + 7)}}{\red{\frac d {dx}(4x^2 + 9x - 1)}}}_{\mbox{L'Hôpital's Rule}} = \displaystyle\lim_{x\to\infty} \frac{\blue{6x - 5}}{\red{8x + 9}} = \frac \infty \infty $$
Step 3Apply L'Hôpital's Rule a second time.
$$ \begin{align*} \lim_{x\to\infty} \frac{6x - 5}{8x + 9} = \lim_{x\to\infty} \frac{\blue{\frac d {dx}(6x - 5)}}{\red{\frac d {dx}(8x + 9)}} = \lim_{x\to\infty} \frac{\blue 6 }{\red 8} = \frac 3 4 \end{align*} $$
Answer$$\displaystyle \lim_{x\to\infty} \frac{3x + 7}{4x + 9} = \frac 3 4$$
For reference, here is a graph of the function.
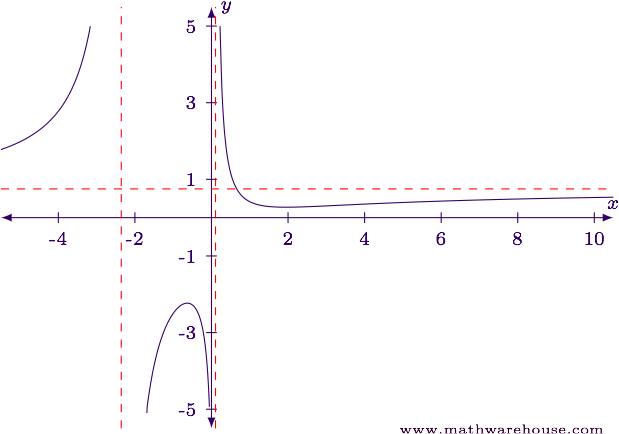
Example 3
Evaluate $$\displaystyle \lim_{x\to 1} \frac{x^2 - 1}{\ln x}$$.
Note that this particular example is not one of the forms from an earlier lesson. So, without L'Hôpital's Rule, we would be hard pressed to evaluate it.
Step 1Evaluate the limit in its current form (to make sure L'Hôpital's Rule applies).
$$ \displaystyle\lim_{x\to 1} \frac{x^2 - 1}{\ln x} = \frac{1^2 - 1}{\ln 1} = \frac 0 0 $$
Step 2Since we have a $$\frac 0 0$$ form, we can use L'Hôpital's rule to try and evaluate it.
$$ \begin{align*} \lim_{x\to 1} \frac{x^2 - 1}{\ln x} & = \lim_{x\to 1} \frac{\blue{\frac d {dx}(x^2 - 1)}}{\red{\frac d {dx}(\ln x)}}\\[6pt] & = \lim_{x\to 1} \frac{\blue{2x}}{\red{1/x}}\\[6pt] & = \lim_{x\to 1} \frac{2x} 1 \cdot \frac x 1&& \hskip -2cm \hspace{8mm} \mbox{(Simplifying is always good.)}\\[6pt] & = \lim_{x\to 1} 2x^2\\[6pt] & = 2(1)^2\\[6pt] & = 2 \end{align*} $$
Answer$$\displaystyle \lim_{x\to 1} \frac{x^2 - 1}{\ln x} = 2$$.
For reference, here is the graph of the function, with the limit value indicated. Note that the function is undefined at $$x=1$$.
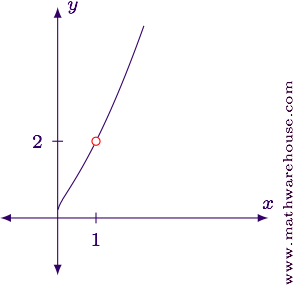
Not A Magic Bullet
It is important to note that L'Hôpital's rule is one tool in our toolbox, but it doesn't help with every limit. In the next lesson we'll look at some examples of limits where applying L'Hôpital's rule isn't appropriate, and we'll discuss what we can do to successfully evaluate such limits.
Proof of L'Hôpital's Rule
As always, before working through the proof, we need to first state the theorem formally.
Formal Statement
Suppose $$\lim\limits_{x\to a}\frac{f(x)}{g(x)}$$ has the form$$\frac 0 0$$ or $$\frac \infty \infty$$. Also, suppose $$f$$ and $$g$$ are continuous in some open interval containing $$x=a$$ (except possibly at $$x=a$$ itself) and neither $$g(x)$$ nor $$g'(x)$$ are equal to zero in that same interval (again, except possibly at $$x=a$$ itself).
Then
$$ \displaystyle\lim_{x\to a} \frac{f(x)}{g(x)} = \displaystyle\lim_{x\to a} \frac{f'(x)}{g'(x)} $$
provided the right-hand limit exists or is $$\pm\infty$$.
Proof:
This proof focuses on the case where $$\lim\limits_{x\to a} \frac{f(x)}{g(x)} = \frac 0 0$$. The case where the limit is $$\frac\infty \infty$$ is approached similarly.
Since $$\lim\limits_{x\to a} f(x) = 0$$, we know that either $$f(a) = 0$$ or $$f$$ has a removable discontinuity at $$x = a$$. In the case where we have the removable discontinuity, we can redefine $$f$$ so that $$f(a) = 0$$ without affecting the value of the limit, so let's do that.
Likewise, the same situation applies to $$g(x)$$ at $$x = a$$, so make the same redefinition if needed. This means we now have $$\blue{f(a) = 0}$$ and $$\red{g(a) = 0}$$, so we can write ...
$$ \begin{align*} \frac{f(x)}{g(x)} & = \frac{f(x) - \blue 0}{g(x) - \red 0}\\[6pt] & = \frac{f(x) - \blue{f(a)}}{g(x) - \red{g(a)}} \end{align*} $$
Since $$f$$ and $$g$$ are differentiable in the neighborhood of $$x=a$$, we can apply Cauchy's extension of the MVT. This means there is a $$c\in(a,x)$$ such that
$$ f'(c) = \frac{f(x)-\blue{f(a)}}{g(x)-\red{g(a)}}\cdot g'(c) $$
Dividing both sides by $$g'(c)$$ gives us
$$ \frac{f'(c)}{g'(c)} = \frac{f(x)-\blue{f(a)}}{g(x)-\red{g(a)}} = \frac{f(x)}{g(x)} $$
If we examine the limit as $$x \to a^+$$, we see that $$c\to a^+$$ as well (since $$c \geq a$$). This means we can say
$$ \displaystyle\lim_{x\to a^+} \frac{f(x)}{g(x)} = \displaystyle\lim_{c\to a^+} \frac{f'(c)}{g'(c)}. $$
As similar argument with $$x \to a^-$$ allows us to say
$$ \displaystyle\lim_{x\to a^-} \frac{f(x)}{g(x)} = \displaystyle\lim_{c\to a^-} \frac{f'(c)}{g'(c)} $$
Finally, the last phrase in the formal statement of L'Hôpital's Rule says that the equation is valid provided the limit on the right exists. In order for this statement to be valid, we know the one-sided limits have to be the same. In that case
$$ \displaystyle\lim_{x\to a^-} \frac{f(x)}{g(x)} = \displaystyle\lim_{c\to a^-} \frac{f'(c)}{g'(c)} = \displaystyle\lim_{x\to a^+} \frac{f(x)}{g(x)} = \displaystyle\lim_{c\to a^+} \frac{f'(c)}{g'(c)} $$
which implies
$$ \displaystyle\lim_{x\to a} \frac{f(x)}{g(x)} = \displaystyle\lim_{x\to a} \frac{f'(x)}{g'(x)} $$
This concludes the proof.
Continue to Practice Problems



















