Evaluate the limit in its current form.
$$ \begin{align*} \lim_{x\to4} \frac{3x^2 - 11x - 4}{2x^2 - 3x - 20} & = \frac{3(4)^2 - 11(4) - 4}{2(4)^2 - 3(4) - 20}\\[6pt] & = \frac{48 - 44 - 4}{32 - 12 - 20}\\[6pt] & = \frac 0 0 \end{align*} $$
Since the limit has the $$\frac 0 0$$ form, we can use L'Hôpital's rule.
$$ \begin{align*} \lim_{x\to4} \frac{3x^2 - 11x - 4}{2x^2 - 3x - 20} & = \lim_{x\to4} \frac{\blue{\frac d {d}(3x^2 - 11x - 4)}}{\red{\frac d {dx}(2x^2 - 3x - 20)}}\\[6pt] & = \lim_{x\to4} \frac{\blue{6x - 11}}{\red{4x - 3}}\\[6pt] & = \frac{6(4)-11}{4(4)-3}\\[6pt] & = \frac{13}{13}\\[6pt] & = 1 \end{align*} $$
$$\displaystyle \lim\limits_{x\to4} \frac{3x^2 - 11x - 4}{2x^2 - 3x - 20} = 1$$
For reference, here is the function with the limit value indicated.
Evaluate the limit in its current form.
$$ \begin{align*} \lim_{x\to 0} \frac{\tan 2x}{3x} & = \frac{\tan 0} 0 = \frac 0 0 \end{align*} $$
Use L'Hôpital's Rule to evaluate the limit.
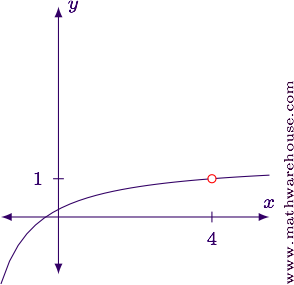
$$ \begin{align*} \lim_{x\to 0} \frac{\tan 2x}{3x} & = \lim_{x\to 0} \frac{\blue{\frac d {dx}(\tan 2x)}}{\red{\frac d {dx}(3x)}}\\[6pt] & = \lim_{x\to 0} \frac{\blue{2\sec^2(2x)}}{\red 3}\\[6pt] & = \frac{2\sec^2(0)}{3}\\[6pt] & = \frac{2(1)} 3\\[6pt] & = \frac 2 3 \end{align*} $$
$$\displaystyle \lim_{x\to 0} \frac{\tan 2x}{3x} = \frac 2 3$$
For reference, here is the graph of the function with the limit point indicated.
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to9}\frac{\sqrt x - 3}{x-9} = \frac{\sqrt 9 - 3}{9-9} = \frac 0 0 $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to9}\frac{\sqrt x - 3}{x-9} & = \lim_{x\to9} \frac{\blue{\frac d {dx}\left(x^{1/2} - 3\right)}}{\red{\frac d {dx}(x-9)}}\\[6pt] & = \lim_{x\to9} \frac{\blue{\frac 1 2 x^{-1/2}}}{\red 1}\\[6pt] & = \lim_{x\to9} \frac 1 {2 x^{1/2}}\\[6pt] & = \lim_{x\to9} \frac 1 {2 \sqrt x}\\[6pt] & = \frac 1 {2 \sqrt 9}\\[6pt] & = \frac 1 6 \end{align*} $$
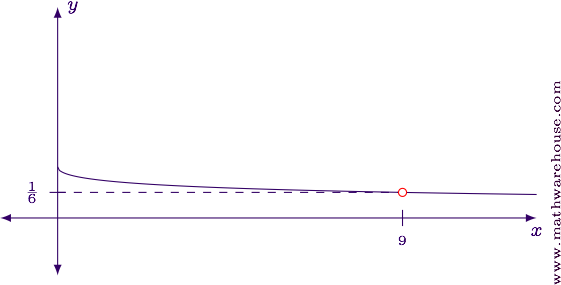
$$ \displaystyle \lim_{x\to9}\frac{\sqrt x - 3}{x-9} = \frac 1 6 $$
For reference, here is the graph of the function with the limit point indicated.
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 8}\frac{2x^2-31x+120}{\sqrt{x+1}-3} = \frac{2(8)^2-31(8)+120}{\sqrt{8+1}-3} = \frac{128 - 248 + 120}{\sqrt 9 - 3} = \frac 0 0 $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 8}\frac{2x^2-31x+120}{\sqrt{x+1}-3} & = \lim_{x\to 8}\frac{\blue{\frac d {dx}(2x^2-31x+120)}}{\red{\frac d {dx}\left((x+1)^{1/2}-3\right)}}\\[6pt] & = \lim_{x\to 8}\frac{\blue{4x-31}}{\red{\frac 1 2 (x+1)^{-1/2}}}\\[6pt] & = \lim_{x\to 8} 2(4x-31)(x+1)^{1/2}\\[6pt] & = 2(4(8)-31)\sqrt{8+1}\\[6pt] & = 2(32-31)\sqrt 9\\[6pt] & = 2(1)(3)\\[6pt] & = 6 \end{align*} $$
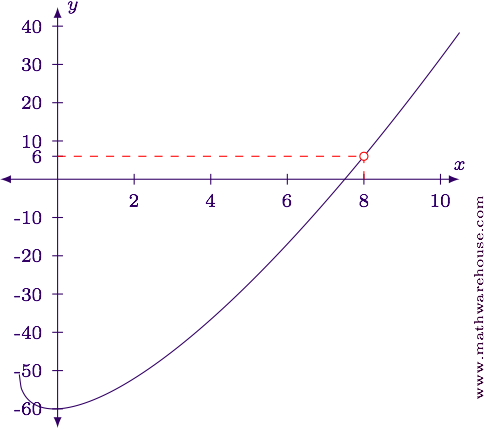
$$ \displaystyle \lim_{x\to 8}\frac{2x^2-31x+120}{\sqrt{x+1}-3} = 6 $$
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 5} \frac{3x^2 - 75}{1/5-1/x} = \frac{3(5^2) - 75}{1/5 - 1/5} = \frac 0 0 $$
Apply L'Hôpital's rule, and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 5} \frac{3x^2 - 75}{1/5-1/x} & = \lim_{x\to 5} \frac{\blue{\frac d {dx}(3x^2 - 75)}}{\red{\frac d {dx}\left(1/5-x^{-1}\right)}}\\[6pt] & = \lim_{x\to 5} \frac{\blue{6x}}{\red{x^{-2}}}\\[6pt] & = \lim_{x\to 5} 6x^3\\[6pt] & = 6(5^3)\\[6pt] & = 750 \end{align*} $$
$$ \displaystyle \lim_{x\to 5} \frac{3x^2 - 75}{1/5-1/x} = 750 $$
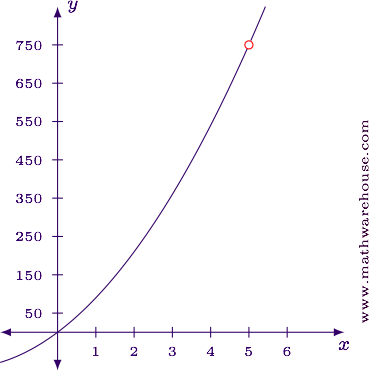
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to0} \frac{3x^2-2x}{3^x-5^x} = \frac{3(0)^2-2(0)}{3^0-5^0} = \frac 0 {1 -1} = \frac 0 0 $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to0} \frac{3x^2-2x}{3^x-5^x} & = \lim_{x\to0} \frac{\blue{\frac d {dx}(3x^2-2x)}}{\red{\frac d {dx}\left(3^x-5^x\right)}}\\[6pt] & = \lim_{x\to0} \frac{\blue{6x-2}}{\red{3^x\ln 3-5^x\ln 5}}\\[6pt] & = \frac{6(0) - 2}{3^0\ln 3 - 5^0\ln 5}\\[6pt] & = \frac{-2}{\ln 3 - \ln 5}\\[6pt] & = \frac 2 {\ln 5 - \ln 3}\\[6pt] & \approx 3.9152 \end{align*} $$
$$ \displaystyle \lim_{x\to0} \frac{3x^2-2x}{3^x-5^x} = \frac 2 {\ln 5 - \ln 3} $$
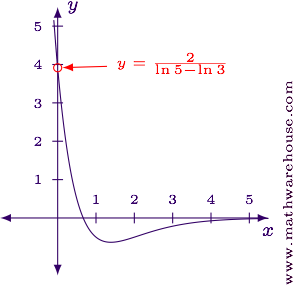
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to0} \frac{\arctan(8x)}{\arcsin(2x)} = \frac{\arctan 0}{\arcsin 0} = \frac 0 0 $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to0} \frac{\arctan(8x)}{\arcsin(2x)} & \lim_{x\to0} \frac{\blue{\frac d {dx}\left(\arctan(8x)\right)}}{\red{\frac d {dx}\left(\arcsin(2x)\right)}}\\[6pt] & = \lim_{x\to0} \frac{\blue{8/(1 + 64x^2)}}{\red{2/\sqrt{1 - 4x^2}}}\\[6pt] & = \lim_{x\to0} \frac 8 {1 + 64x^2}\cdot \frac {\sqrt{1 - 4x^2}} 2\\[6pt] & = \lim_{x\to0} \frac{4\sqrt{1-4x^2}}{1 + 64x^2}\\[6pt] & = \frac{4\sqrt{1-4(0^2)}}{1+64(0^2)}\\[6pt] & = \frac {4\sqrt 1} 1\\[6pt] & = 4 \end{align*} $$
$$ \displaystyle \lim_{x\to0} \frac{\arctan(8x)}{\arcsin(2x)} = 4\ $$
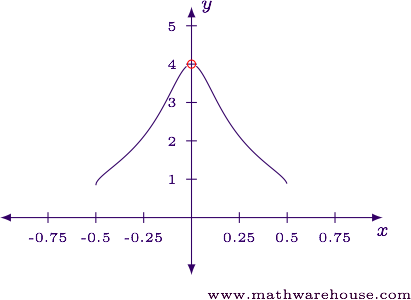
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to0} \frac{x^2e^{0.5x}}{\tan^2(0.75x)} = \frac{0\cdot 1}{0^2} = \frac 0 0 $$
Applying L'Hôpital's rule to this particular function will result in an ugly mess. Instead, start by rewriting the tangent in terms of sines and cosines.
$$ \displaystyle\lim_{x\to0} \frac{x^2e^{0.5x}}{\tan^2(0.75x)} = \displaystyle\lim_{x\to0} \frac{x^2e^{0.5x}}{\sin^2(0.75x)/\cos^2(0.75x)} =\displaystyle\lim_{x\to0} \frac{x^2\cos^2(0.75x)e^{0.5x}}{\sin^2(0.75x)} $$
Group the cosines and the exponential function into their own limit.
$$ \displaystyle\lim_{x\to0} \frac{x^2\cos^2(0.75x)e^{0.5x}}{\sin^2(0.75x)} = \displaystyle\lim_{x\to0} \frac{x^2}{\sin^2(0.75x)}\cdot \displaystyle\lim_{x\to0} \cos^2(0.75x)e^{0.5x} $$
Evaluate the limit in its current form.
$$ \begin{align*}% \blue{\lim_{x\to0} \frac{x^2}{\sin^2(0.75x)}}\cdot \red{\lim_{x\to0} \cos^2(0.75x)e^{0.5x}} & = \blue{\frac{0^2}{\sin^2 0}}\cdot \red {\cos^2 0\cdot e^0}\\[6pt] & = \blue{\frac 0 0} \cdot \red 1 \end{align*} $$
We can see that the second limit (of the cosine and exponential functions) will not affect the value of the overall limit, so we turn our attention to the $$\blue{\frac 0 0}$$ form and apply L'Hôpital's rule.
$$ \begin{align*} \lim_{x\to0} \frac{x^2}{\sin^2(0.75x)} & = \lim_{x\to0} \frac{\blue{\frac d {dx}(x^2)}}{\red{\frac d {dx}\left(\sin^2 0.75x\right)}}\\[6pt] & = \lim_{x\to0} \frac{\blue{2x}}{\red{2\sin(0.75x)\cos(0.75x)\cdot 0.75}}\\[6pt] & = \lim_{x\to0} \frac{2x}{1.5\sin(0.75x)\cos(0.75x)}\\[6pt] & = \frac{0}{1.5\sin 0\cdot \cos 0}\\[6pt] & = \frac 0 0 \end{align*} $$
Again, group the cosine into its own limit.
$$ \begin{align*}% \lim_{x\to0} \frac{2x}{1.5\sin(0.75x)\cos(0.75x)} & = \blue{\lim_{x\to0} \frac{2x}{1.5\sin 0.75x }}\cdot \red{\lim_{x\to0} \frac 1 {\cos 0.75x}}\\[6pt] & = \blue{\frac{0}{1.5\sin 0}}\cdot \red{\frac 1 {\cos 0}}\\[6pt] & = \blue{\frac 0 0} \cdot \red 1 \end{align*} $$
As before, the cosine isn't going to contribute to the value of the limit, so we focus on the $$\blue{\frac 0 0}$$ form and apply L'Hôpital's rule.
$$ \begin{align*} \lim_{x\to0} \frac{2x}{1.5\sin(0.75x)} & = \lim_{x\to0} \frac{\blue{\frac d {dx}(2x)}}{\red{\frac d {dx}(1.5\sin 0.75x)}}\\[6pt] & = \lim_{x\to0} \frac{\blue 2}{\red{1.5\cos(0.75x)\cdot 0.75}}\\[6pt] & = \lim_{x\to0} \frac 2 {1.125\cos 0.75x}\\[6pt] & = \lim_{x\to0} \frac 2 {1.125\cos 0}\\[6pt] & = \frac 2 {1.125}\\[6pt] & = \frac{16} 9\\[6pt] & \approx 1.78 \end{align*} $$
$$\displaystyle \lim_{x\to0} \frac{x^2e^{0.5x}}{\tan^2(0.75x)} = \frac{16} 9$$
In the interest of full disclosure, after we completed Step 3, we didn't have to use L'Hôpital's Rule. We could have used the techniques we learned earlier in the lesson on Indeterminate Limits---Sine Forms and in fact, that technique would have been much less work!
For reference, here is the graph along with the limit value.
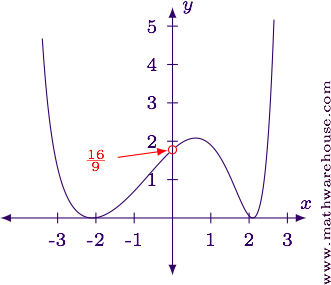
Evaluate the limit in its current form.
$$ \begin{align*} \lim_{x\to\infty} \frac{4x^3+6x^2-9x+1}{2x^3-5x^2+8} & = \frac \infty \infty \end{align*} $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to\infty} \frac{4x^3+6x^2-9x+1}{2x^3-5x^2+8} & = \lim_{x\to\infty} \frac{\blue{\frac d {dx}(4x^3+6x^2-9x+1)}}{\red{\frac d {dx}(2x^3-5x^2+8)}}\\[6pt] & = \lim_{x\to\infty} \frac{\blue{12x^2+12x-9}}{\red{6x^2-10x}}\\[6pt] = \frac \infty \infty \end{align*} $$
Though we still obtained an indeterminate form for the limit, we notice that the degrees of the numerator and denominator have reduced by 1. It is reasonable to expect that repeated applications of L'Hôpital's rule will continue to reduce the degrees of the function until we no longer have an indeterminate form.
Apply L'Hôpital's rule repeatedly, checking the limit after each application, until we no longer have an indeterminate form.
L'Hôpital's Rule (2nd Time)
$$ \begin{align*}% \lim_{x\to\infty} \frac{12x^2+12x-9}{6x^2-10x} & =\lim_{x\to\infty} \frac{\blue{\frac d {dx}(12x^2+12x-9)}}{\red{\frac d {dx}(6x^2-10x)}}\\[6pt] & = \lim_{x\to\infty} \frac{\blue{24x+12}}{\red{12x-10}}\\[6pt] & = \lim_{x\to\infty} \frac{12x+6}{6x-5}\\[6pt] & = \frac \infty \infty \end{align*} $$
L'Hôpital's Rule (3rd Time)
$$ \displaystyle\lim_{x\to\infty} \frac{12x+6}{6x-5} = \displaystyle\lim_{x\to\infty} \frac{\blue{\frac d {dx}(12x+6)}}{\red{\frac d {dx}(6x-5)}} = \displaystyle\lim_{x\to\infty} \frac{\blue{12}}{\red 6} = \frac {12} 6 = 2 $$
$$ \displaystyle \lim_{x\to\infty} \frac{4x^3+6x^2-9x+1}{2x^3-5x^2+8} = 2 $$
As in the previous exercise, this particular limit is much easier to evaluate using techniques learned in a previous lesson (Limits At Infinity---Rational Forms).
So, while this question provided good practice with L'Hôpital's Rule, the moral of the story is: Just because it works, doesn't mean its efficient!
Here, for reference, is the graph along with the limiting value indicated.
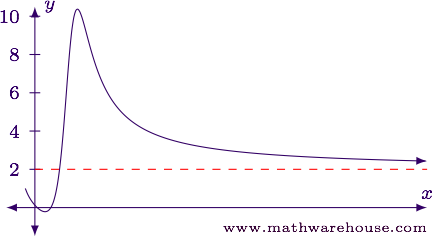
Evaluate the limit in its current form.
Since $$ e^{x^2} $$ grows exponentially and $$ x^2+1 $$ grows quadratically, we have
$$ \lim_{x\to\infty} \frac{e^{x^2}}{x^2+1}= \frac\infty \infty $$
Since the limit has the form $$\frac \infty \infty$$ we can use L'Hôpital's rule to help evaluate it.
$$ \begin{align*} \lim_{x\to\infty} \frac{e^{x^2}}{x^2+1} & = \lim_{x\to\infty} \frac{\blue{\frac d {dx}\left(e^{x^2}\right)}}{\red{\frac d {dx}(x^2+1)}}\\[6pt] & = \lim_{x\to\infty} \frac{\blue{2xe^{x^2}}}{\red{2x}}\\[6pt] & = \lim_{x\to\infty} \frac{e^{x^2}}{1}\\[6pt] & = \infty \end{align*} $$
$$\displaystyle \lim_{x\to\infty} \frac{e^{x^2}}{x^2+1} = \infty$$, which of course means the limit does not exist.
For reference, here is the graph of the function.
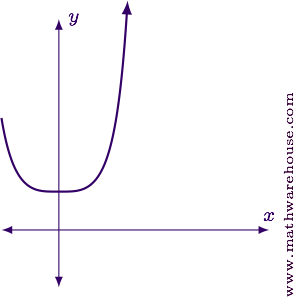
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to\infty} \frac{e^{2x}-5x}{3x^2 + 8x} = \frac \infty \infty $$
Apply L'Hôpital's rule, and re-evaluate the limit.
$$ \displaystyle\lim_{x\to\infty} \frac{e^{2x}-5x}{3x^2 + 8x} = \displaystyle\lim_{x\to\infty} \frac{\blue{\frac d {dx}(e^{2x}-5x)}}{\red{\frac d {dx}(3x^2 + 8x)}} = \displaystyle\lim_{x\to\infty} \frac{\blue{2e^{2x}-5}}{\red{6x + 8}} = \frac \infty \infty $$
Apply L'Hôpital's rule a second time, and re-evaluate the limit again.
$$ \displaystyle\lim_{x\to\infty} \frac{2e^{2x}-5}{6x + 8} = \displaystyle\lim_{x\to\infty} \frac{\blue{\frac d {dx}(2e^{2x}-5)}}{\blue{\frac d {dx}(6x + 8)}} = \displaystyle\lim_{x\to\infty} \frac{\blue{4e^{2x}}}{\red 6} = \lim_{x\to\infty} \frac 2 3e^{2x} = \infty $$
$$ \displaystyle\lim_{x\to\infty} \frac{e^{2x}-5x}{3x^2 + 8x} = \infty $$
For reference, here is the graph of the function.
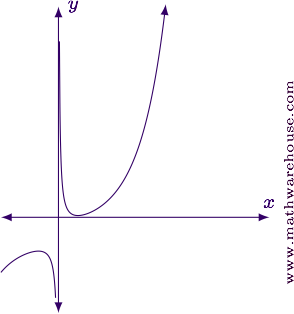
Evaluate both limits in their current form.
The arctangent function has two horizontal asymptotes. As shown in the graph below the arctangent approaches a value of $$\frac \pi 2$$ as $$x \to \infty$$. But as $$x\to-\infty$$, the arctangent approaches $$-\frac \pi 2$$.
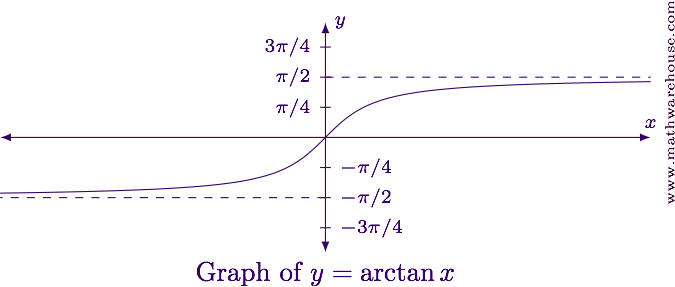
With this in mind, we can evaluate the two limits as follows.
$$ \begin{align*} (a) \qquad \lim_{x\to\infty} \frac{3\pi - 6\arctan(9x)}{2\arctan(3x)-\pi} & = \frac{3\pi - 6\left(\frac \pi 2\right)}{2\left(\frac \pi 2\right) - \pi} = \frac{3\pi - 3\pi}{\pi - \pi} = \frac 0 0\\[12pt] (b)\qquad \lim_{x\to\infty} \frac{3\pi - 6\arctan(9x)}{2\arctan(3x)-\pi} & = \frac{3\pi - 6\left(-\frac \pi 2\right)}{2\left(-\frac \pi 2\right) - \pi} = \frac{3\pi + 3\pi}{-\pi - \pi} = \frac{6\pi}{-2\pi} = 3 \end{align*} $$
Only the first of these limits is indeterminate, so we will only need L'Hôpital's rule for it.
Use L'Hôpital's rule, then re-evaluate the limit.
$$ \begin{align*} \lim_{x\to\infty} \frac{3\pi-6\arctan(9x)}{2\arctan(3x)-\pi} & = \lim_{x\to\infty} \frac{\blue{\frac d {dx}(3\pi-6\arctan 9x)}}{\red{\frac d {dx}(2\arctan(3x)-\pi)}}\\[6pt] & = \lim_{x\to\infty} \frac{\blue{0-6\cdot\frac 1 {1 + (9x)^2}\cdot 9}}{\red{2\cdot \frac 1 {1 + (3x)^2}\cdot 3-0}}\\[6pt] & = \lim_{x\to\infty} \frac{-\frac{54}{1 + 81x^2}}{\frac 6 {1 + 9x^2}}\\[6pt] & = \lim_{x\to\infty} -\frac{54}{1 + 81x^2}\cdot\frac{1 + 9x^2} 6\\[6pt] & = \lim_{x\to\infty} -\frac{9(1 + 9x^2)}{1 + 81x^2}\\[6pt] & = \lim_{x\to\infty} -\frac{9 + 81x^2}{1 + 81x^2}\\[6pt] & = -\frac{81}{81}\\[6pt] & = -1 \end{align*} $$
Note that the final form of the limit could be evaluated with two more applications of L'Hôpital's Rule, but it is much quicker to use the techniques discussed in earlier lessons.
(a) $$\displaystyle \lim_{x\to\infty} \frac{3\pi - 6\arctan(9x)}{2\arctan(3x)-\pi} = -1$$ and (b) $$\displaystyle \lim_{x\to-\infty} \frac{3\pi - 6\arctan(9x)}{2\arctan(3x)-\pi} = -3$$
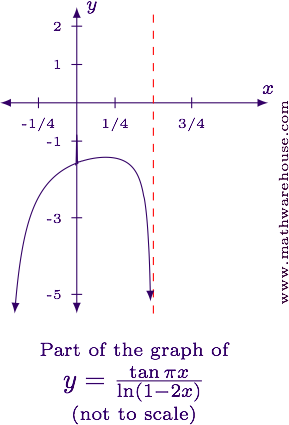
Evaluate the limit in its current form.
$$ \begin{align*} \lim_{x\to 1/2^-} \frac{\tan \pi x}{\ln(1 - 2x)} & = \lim_{x\to 1/2^-} \frac{\tan \frac \pi 2}{\ln 0}\\[6pt] & = \frac \infty \infty \end{align*} $$
Use L'Hôpital's Rule.
$$ \begin{align*} \lim_{x\to 1/2^-} \frac{\tan \pi x}{\ln(1 - 2x)} & = \lim_{x\to 1/2^-} \frac{\blue{\frac d {dx}(\tan \pi x)}}{\red{\frac d {dx}\left(\ln(1 - 2x)\right)}}\\[6pt] & = \lim_{x\to 1/2^-} \frac{\blue{\pi\,\sec^2 \pi x}}{\red{\frac{-2}{1-2x}}}\\[6pt] & = \lim_{x\to 1/2^-} \frac{\pi\,\sec^2 \pi x} 1 \cdot \frac{1-2x}{-2}\\[6pt] & = \lim_{x\to 1/2^-} \frac \pi {\cos^2 \pi x}\cdot \frac{1-2x}{-2}\\[6pt] & = \lim_{x\to 1/2^-} \frac{\pi(2x-1)}{2\cos^2\pi x}\\[6pt] & = \frac 0 0 \end{align*} $$
Apply L'Hôpital's Rule a 2nd time..
$$ \begin{align*} \lim_{x\to 1/2^-} \frac{\pi(2x-1)}{2\cos^2\pi x} & = \lim_{x\to 1/2^-} \frac \pi 2 \cdot \frac{\blue{\frac d {dx}(2x-1)}}{\red{\frac d {dx}(\cos^2\pi x)}}\\[6pt] & = \lim_{x\to 1/2^-} \frac \pi 2 \cdot \frac{\blue 2}{\red{-2\pi\sin \pi x\cos\pi x}}\\[6pt] & = \lim_{x\to 1/2^-} -\frac 1 {2\sin \pi x\cos\pi x}\\[6pt] & = -\frac 1 {2\sin 0\cdot \cos 0}\\[6pt] & = -\frac 1 0 \end{align*} $$
Since the denominator approaches 0, but the numerator doesn't, this function becomes infinitely large (in the negative direction).
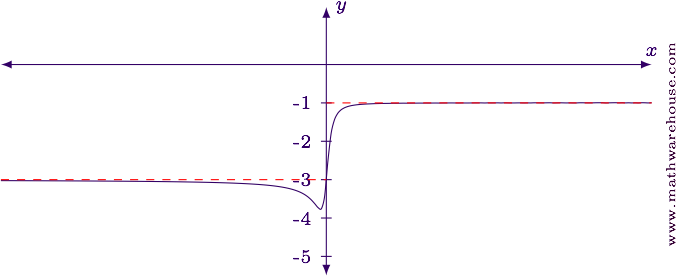
$$\displaystyle \lim_{x\to 1/2^-} \frac{\tan \pi x}{\ln(1 - 2x)} = -\infty$$ (i.e., the limit doesn't exist because the function grows without bound).
For reference, here is the graph of the function.
Evaluate the limit in its current form.
Since $$p>0$$, we know $$x^p$$ will increase without bound as $$x$$ increases.
Likewise, since $$b>1$$, we know $$b^x$$ describes exponential growth, so it also increases without bound as $$x$$ increases. Consequently,
$$ \displaystyle\lim_{x\to\infty} \frac{x^p}{b^x} = \frac \infty \infty. $$
Apply L'Hôpital's Rule and re-evaluate the limit. Repeat as needed.
Without an explicit value for $$p$$, we can't know how many times L'Hôpital's Rule will be needed. Consequently, I'm going to set up a table to keep track of each iteration.
$$ \def\arraystretch{2.2} \begin{array}{clc} {\textbf{Iteration}} & {\textbf{Limit from L'Hôpital's Rule}} & {\textbf{Limit Value}}\\ \hline 1 & \lim\limits_{x\to\infty} \frac{px^{p-1}}{\ln b\cdot b^x} & \frac \infty \infty\\ 2 & \lim\limits_{x\to\infty} \frac{p(p-1)x^{p-2}}{(\ln b)^2\cdot b^x} & \frac \infty \infty\\ 3 & \lim\limits_{x\to\infty} \frac{p(p-1)(p-2)x^{p-3}}{(\ln b)^3\cdot b^x} & \frac \infty \infty\\ \vdots & \vdots & \vdots\\ n & \lim\limits_{x\to\infty} \frac{p(p-1)(p-2)\dots(p - (n-1))x^{p-n}}{(\ln b)^n\cdot b^x} & \frac \infty \infty\\ \hline \end{array} $$
Here's what we see in the table above. Every time we use L'Hôpital's Rule, the exponent in the numerator goes down by 1. No matter what value of $$p$$ we start with, enough iterations of the rule will result in the exponent on $$x$$ becoming zero, or negative. But in the denominator the function always behaves like $$b^x$$.
When $$n = p$$.
If the original exponent on $$x$$ is an integer, then eventually (when we've applied L'Hôpital's Rule enough times), we will end up with $$0$$ for an exponent on $$x$$. In that case, the limit would be
$$ \displaystyle\lim_{x\to\infty} \frac{p(p-1)(p-2)\dots(2)(1)x^0}{(\ln b)^p\cot b^x} \displaystyle\lim_{x\to\infty} \frac{p(p-1)(p-2)\dots(2)}{(\ln b)^p\cdot b^x} = \frac{\mbox{constant}}{\infty} $$
Since the numerator is becomes a constant, but the numerator grows infinitely large, the entire function approaches $$0$$.
When $$p-n<0$$.
However, if the original exponent on $$x$$ isn't an integer, the exponent will eventually become negative. Let's look at what happens to the limit as soon as $$x$$ has a negative exponent. Let's use $$-k$$ to represent this negative exponent. (Note, I've left out the coefficients because they aren't going to affect the behavior of the function as $$x\to \infty$$.)
$$ \displaystyle\lim_{x\to\infty} \frac{x^{-k}}{b^x} = \displaystyle\lim_{x\to\infty} \frac 1 {x^k\cdot b^x} = \frac 1 \infty $$
Again, we see that the denominator of the function becomes larger, but the numerator is constant, so the function is approaching zero.
For any $$p>0$$ and $$b>1$$, $$\displaystyle \lim_{x\to\infty} \frac{x^p}{b^x} = 0$$.
For reference (and to facilitate the discussion in the next part of the solution) the graph below shows three functions. For $$p = 10$$, and $$b = 2$$ we have
\begin{align*} \color{importantColor}{f(x)} & \color{importantColor}{= x^3}\\ \color{secondaryColor}{g(x)} & \color{secondaryColor}{= 2^x}\\ \color{graphColor}{y} & \color{graphColor}{= \frac{x^3}{2^x}} \end{align*}
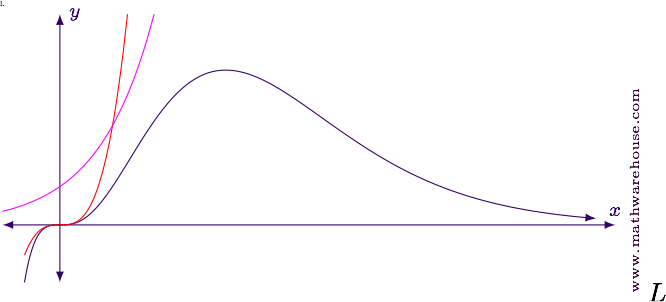
In part (a) we showed that $$\lim\limits_{x\to\infty} \frac{x^p}{b^x} = 0$$ as long as $$p>0$$ and $$b>1$$. What this tells us is that any exponential growth function (no matter how small the base) will grow faster than any power function of the form $$x^p$$ no matter how large the exponent.
Think about it this way. How fast would $$f(x) = x^{\mbox{one million}}$$ increase as $$x$$ gets bigger? Answer? Really fast. If you graph this function near the origin, it looks like a vertical line and by the time $$x = 2$$ the $$f(x)$$-value is $$2^{\mbox{one million}}$$ which is HUGE.
By contrast, $$g(x) = 1.000001^x$$ grows (at first) so slowly that it's graph (near the origin) looks like a horizontal line. It seems impossible that this function could ever intersect, and then become larger than the first one.
But that's exactly what we've proven! No matter how big the exponent of a power function, any exponential growth function will eventually surpass it in value!
(Just as a side note, the two example functions intersect when $$x \approx 3.10672\times 10^{13}$$ and $$y~\approx~1.29798\times 10^{1{,}3492{,}302}$$.)
Evaluate the limit in it current form.
Like in Question 14(a), we know $$x^p$$ will increase infinitely large since $$p>0$$.
And since $$b>1$$ we know $$\log_b x$$ will also increase without bound. Consequently
$$ \displaystyle\lim_{x\to \infty} \frac{\log_b x}{x^p} = \frac \infty \infty $$
Apply L'Hôpital's Rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to \infty} \frac{\log_b x}{x^p} & = \lim_{x\to \infty} \frac{\frac{\ln x}{\ln b}}{x^p} && \hskip -2cm \hspace{15mm} \mbox{Change of Base Formula}\\[6pt] & = \lim_{x\to \infty} \frac{\ln x}{\ln b\cdot x^p}\\[6pt] & = \frac 1 {\ln x}\,\lim_{x\to \infty} \frac{\blue{\frac d {dx}(\ln x)}}{\red{\frac d {dx}(x^p)}}\\[6pt] & = \frac 1 {\ln x}\,\lim_{x\to \infty} \frac{\blue{\frac 1 x}}{\red{px^{p-1}}}\\[6pt] & = \frac 1 {\ln x}\,\lim_{x\to \infty} \frac 1{x\cdot px^{p-1}}\\[6pt] & = \frac 1 {\ln x}\,\lim_{x\to \infty} \frac 1{px^p}\\[6pt] & = \frac 1 {\ln x}\cdot \frac 1 \infty \end{align*} $$
Since the denominator grows infinitely large, but the numerator is finite, this function much approach 0 as $$x$$ grows infinitely large.
$$\displaystyle \lim_{x\to \infty} \frac{\log_b x}{x^p} = 0$$ for any $$p>0$$ and $$b>1$$.
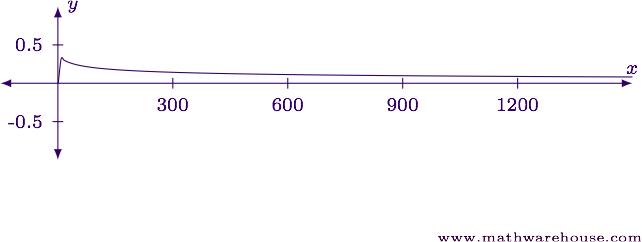
For reference, below is the graph of $$\displaystyle y = \frac{\log_{10}x}{x^{1/2}}$$. Notice how slowly the function converges to zero.
In part (a) we showed that $$\lim\limits_{x\to\infty} \frac{\log_b x}{x^p} = 0$$ as long as $$b>1$$ and $$p>0$$. This means that no matter how small the exponent is, $$y=x^p$$ will eventually become large and grow faster than any logarithmic function.
Since the power just has to be positive, we can use fractional exponents, which are equivalent to root functins (square roots, cube roots, etc.). So we could compare a function, say $$y = \sqrt[100] x$$ or $$y = \sqrt[1000] x$$ to a logarithmic function, and the 100th (or 1000th) root would grow faster than the logarithm!




















