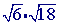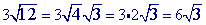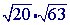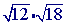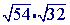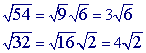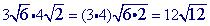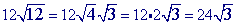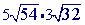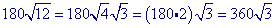Vocabulary Refresher
The radicand refers to the number under the radical sign. In the radical below, the radicand is the number '5'.

Examples
Example 1 of Multiplying Square roots
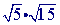 Step 1
Step 1
Check to see if you can simplify either of the square roots (
 ). If you can, then simplify!
). If you can, then simplify!
Both square roots are already simplified so skip this step.
Multiply the radicands together.
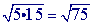
Example 2. A slightly more complex example
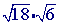 Step 1
Step 1
Check to see if you can simplify either of the square roots(
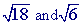 ). If you can, then simplify!
). If you can, then simplify!
 can indeed be simplified:
can indeed be simplified:
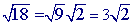
Multiply the radicands together.
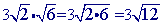
Practice Problems
Multiply the square roots below and express each answer in simplest radical form.
Problem 1
This problem is similar to example 1 because you can not simplify either of the square roots.
Step 1Multiply.
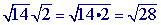
Problem 2
Problem 3
Problem 4
This problem is similar to example 2 because the square roots can be simplified. The only difference is that both square roots, in this problem, can be simplified.
Step 1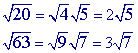
Multiply.
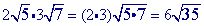
Problem 5
This problem is similar to example 2 because the square roots can be simplified. The only difference is that both square roots, in this problem, can be simplified.
Step 1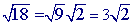
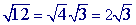
Multiply.
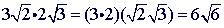
Problem 6
Problem 7
You may notice that this is the same as the problem prior problem (#6)...except that we have now added some coefficients.
Step 1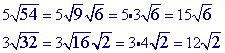
Multiply.
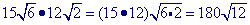

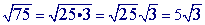
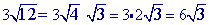
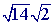
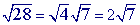
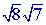
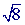 can be simplified:
can be simplified:
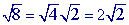
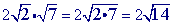
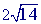 is already in simplest form so you are done.
is already in simplest form so you are done.