Students are often asked to find the equation of a line that is perpendicular to another line and that passes through a point. Watch the video tutorial below to understand how to do these problems and, if you want, download this free worksheet if you want some extra practice.
Practice Problems
Problem 1
Step 1
Find negative reciprocal of the slope:
Slope = -1 or $$-\frac{1}{1} $$
Negative reciprocal = $$\frac{1}{1} = 1$$
Step 2
Plug the x and y given in the equation into the slope interecept formula.
$$0 = 1\left(0\right) + b$$
Step 3
Solve for b.
$$0 = 0 + b$$
$$b = 0$$
Step 4
Substitute b = 0 into slope-intercept equation.
$$y = x$$
Problem 2
Step 1
Find negative reciprocal of the slope:
Slope = 5 or $$\frac{5}{1} $$
Negative reciprocal = $$-\frac{1}{5} $$
Step 2
Plug the x and y given in the equation into the slope interecept formula.
$$ 1= -\frac{1}{5} \left(0\right) + b$$
Step 3
Solve for b.
$$ 1 = 0 + b$$
$$ b = 1$$
Step 4
Substitute b = 1 into slope-intercept equation.
$$y = -\frac{1}{5} x + 1$$
Problem 3
Step 1
Find the negative reciprocal of the slope.
Slope = $$\frac{1}{4} $$
Negative reciprocal = $$-\frac{4}{1} = -4$$
Step 2
Plug the x and y given in the question into the slope interecept formula.
$$ -4 = -4(-4) + b$$
Step 3
Solve for b.
$$ -4 = 16 + b$$
$$ -16 -16$$
$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_$$
$$b = -20$$
Step 4
Substitute b into slope-intercept formula.
$$y = -4x - 20$$
Problem 4
Step 1
Line $$y = -8$$ is parallel to the x-axis. So, the perpendicular line to this line must be parallel to the y-axis.
Step 2
The equation of the perpendicular line is in the form $$x = n$$.
Step 3
This line is perpendicular to the first line at $$y = -8$$; therefore, the second line must be perpendicular at a point with the x-coordinate of -8. That is, $$x = -8$$.
Problem 5
Step 1
Find the negative reciprocal of the slope.
Slope = -3 or $$-\frac{3}{1} $$
Negative reciprocal = $$\frac{3}{1} = 3$$
Step 2
Plug the x and y given in the question into the slope interecept formula.
$$ -5 = 3(0) + b$$
Step 3
Solve for b.
$$-5 = 0 + b$$
$$b = -5$$
Step 4
Substitute b into slope-intercept formula.
$$y = 3x - 5$$
Practice Problems II
Problem 6
Step 1
Line $$x = 32$$ is a vertical line. Any line to be perpendicular to this line must be horizontal.
Step 2
We can draw infinite number of perpendicular lines to this line. Some of them are, for example.
$$y = 21$$
$$y = 22$$
$$y = 23$$
$$y = 24$$
$$\dots \dots$$
$$\dots \dots$$
$$\dots \dots$$
$$y = 32$$
Step 3
Out of all the infinite number of perpendicular lines only one passes through (-32, 32).
Therefore, $$y = -32$$ is the only perpendicular line the problem asked for.
Problem 7
Step 1
Multiply both sides of the equation by 3.
$$3\left(\frac{x+y}{3} \right) = 3 $$
Step 2
Simplify the product on the left.
$$x + y = 3$$
Step 3
Subtract x from each side.
$$x + y - x = 3 - x$$
Step 4
Cancel out the x' on the left.
$$y = -x + 3$$
Step 5
Find the negative reciprocal of the slope.
Slope = -1 or $$-\frac{1}{1} $$
Negative reciprocal = $$\frac{1}{1} =1$$
Step 6
Plug the x and y given in the question into the slope interecept formula.
$$ 6 = 1(-3) + b$$
Step 7
Solve for b.
$$6 = -3 + b$$
$$ +3 +3$$
$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_$$
$$9 = b$$
Step 8
Substitute b into slope-intercept formula.
$$y = x + 9$$
Problem 8
Step 1
Find the slope of the given line first. The line is not in slope-Intercept Form. Add -3x + 5 to both sides.
Step 2
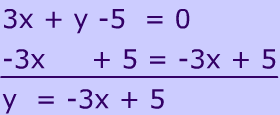
Find the negative reciprocal of the slope.
Slope = -3 or $$-\frac{3}{1} $$
Negative reciprocal = $$\frac{3}{1} =3$$
Step 3
Plug the x and y given in the question into the slope interecept formula.
$$5 = 3(0) + b$$
Step 4
Solve for b.
$$5 = 0 + b$$
$$5 = b$$
Step 5
Substitute b into slope-intercept formula.
$$y = 3x + 5$$
Problem 9
Step 1
The slopes of the lines are as follows:
A: -7
B: $$\frac{1}{7} $$
C: $$-\frac{1}{7} $$
D: $$\frac{1}{7} $$
Step 2
Only the products of the slopes of the following pairs give -1.
$$(Slope of A)(Slope of B) = -1$$
$$(Slope of A)(Slope of D) = -1$$
Step 3
Check the given point to see which lines it fits. Replace (-2, 4) in A.
$$4 = -7(-2) - 10$$
$$4 = 14 - 10$$
$$4 = 4$$
Step 4
So, A is acceptable as one of the perpendicular lines.
Replace (-2, 4) in B.
$$4=\frac{1}{7} (-2)+12$$
$$4=\frac{-2}{7} +12$$
$$4=\frac{-2+84}{7}$$
$$4=\frac{82}{7}$$
Step 5
Both sides are not equal. Thus, line B is not accepted.
Replace (4, -2) in D.
$$4=\frac{1}{7} \left(-2\right)+\frac{30}{7}$$
$$4=\frac{-2}{7} +\frac{30}{7}$$
$$4=\frac{-2+30}{7}$$
$$4=\frac{28}{7}$$
$$4=4$$
Both sides are equal. So, the given point is on D.
Step 6
Point (4, -2) fits two perpendicular lines A and D. Therefore, A and D only are perpendicular lines at (2, -4).
Problem 10
Step 1
All the equations are not in the form of $$y = mx + b$$. So, we must change their forms to y = mx + b first.
Step 2
Equation K: Add 2x to both sides.
$$-2x + 8y + 2x = 11 + 2x$$
Step 3
Cancel out the similar terms on the left side.
$$8y = 2x + 11$$
Step 4
Divide both sides by 8.
$$\frac{8y}{8} =\frac{2x}{8} +\frac{11}{8}$$
Step 5
Simplify the fractions.
$$y=\frac{1}{4} x+\frac{11}{8}$$
Thus, the slope of K is $$\frac{1}{4} $$.
Step 6
L: $$y = 5x - 6$$
This line is already in Slope-Intercept form. The coefficient of x is 5.
L: slope is 5.
Step 7
M: $$-x = 4y + 12$$
This line is not in slope-intercept form. Subtract 12 from each side.
$$-x - 12 = 4y + 12 - 12$$
Step 8
Cancel out numbers on the right side.
$$-x - 12 = 4y$$
Step 9
Divide both sides by 4.
$$\frac{x}{4} -\frac{12}{4} =\frac{4y}{4}$$
Step 10
Simplify all the fractions.
$$y=-\frac{1}{4} x-3$$
That is, the slope of M is $$-\frac{1}{4} $$.
Step 11
N: $$y = -4x + 9$$ is in slope -- intercept form.
The coefficient of x is the slope of the line. Thus, -4 is the slope of N.
Step 12
Now we have four slopes:
Slope of $$K = \frac{1}{4} $$
Slope of $$L = 5$$
Slope of $$M = -\frac{1}{4} $$
Slope of $$N = -4$$
The product of the slopes of K and N is $$\left(\frac{1}{4} \right)\left(-4\right)=-1$$. So K and N are perpendicular.
