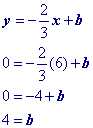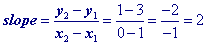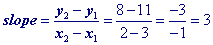Part I. How Linear Equations relate to Tables Of Values
Equations as Relationships
The equation of a line expresses a relationship between x and y values on the coordinate plane. For instance, the equation $$y = x$$ expresses a relationship where every x value has the exact same y value. The equation $$ y = 2x $$ expresses a relationship in which every y value is double the x value, and $$ y = x + 1 $$ expresses a relationship in which every y value is 1 greater than the x value.
So what about a Table Of Values?
Since, as we just wrote, every linear equation is a relationship of x and y values, we can create a table of values for any line. These are just the $$ x $$ and $$ y $$ values that are true for the given line. In other words, a table of values is simply some of the points that are on the line.
Example 1
Equation: $$ \red y = \blue x + 1 $$
Table of Values
| $$ \blue x \text { value} $$ | Equation | $$ \red y \text{ value} $$ |
| y = x + 1 | ||
| $$ \blue 3 $$ | $$y = ( \blue 3 ) + 1$$ | $$ \red 4 $$ |
| $$ \blue 4 $$ | y = ($$ \blue 4 $$ ) + 1 | $$ \red 5 $$ |
| $$ \blue 5 $$ | $$ y = (\blue 5 ) + 1$$ | $$ \red 6 $$ |
| $$ \blue 6 $$ | $$ y = ( \blue 6) + 1 $$ | $$ \red 7 $$ |
Example 2
Equation: y = 3x + 2
Table of Values
| X Value | Equation | Y value |
| y = 3x + 2 | ||
| 1 | y = 3(1) + 2 | 5 |
| 2 | y = 3(2) + 2 | 7 |
| 3 | y = 3(3) + 2 | 11 |
| 4 | y = 3(4) + 2 | 14 |
So, to create a table of values for a line, just pick a set of x values, substitute them into the equation and evaluate to get the y values.
Practice Creating a Table of Values
Problem 1
Create a table of values of the equation y = 5x + 2.
Create the table and choose a set of x values.
| X Value | Equation | Y value |
| y = 5x + 2 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Substitute each x value (left side column) into the equation.
| X Value | Equation | Y value |
| y = 5x + 2 | ||
| 1 | y = 5(1) + 2 | |
| 2 | y = 5(2) + 2 | |
| 3 | y = 5(3) + 2 | |
| 4 | y = 5(4) + 2 |
Evaluate the equation (middle column) to arrive at the y value.
| X Value | Equation | Y value |
| y = 5x + 2 | ||
| 1 | y = 5(1) + 2 | 7 |
| 2 | y = 5(2) + 2 | 12 |
| 3 | y = 5(3) + 2 | 17 |
| 4 | y = 5(4) + 2 | 22 |
An Optional step, if you want, you can omit the middle column from your table, since the table of values is really just the x and y pairs.
(We used the middle column simply to help us get the y values)
| X Value | Y Value |
| 1 | 7 |
| 2 | 12 |
| 3 | 17 |
| 4 | 22 |
Problem 2
Create a table of values of the equation y = −6x + 2.
Create the table and choose a set of x values.
| X Value | Equation | Y value |
| y = −6x + 2 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Substitute each x value (left side column) into the equation.
| X Value | Equation | Y value |
| y = −6x + 2 | ||
| 1 | y = −6(1) + 2 | |
| 2 | y = −6(2) + 2 | |
| 3 | y = −6(3) + 2 | |
| 4 | y = −6(4) + 2 |
Evaluate the equation (middle column) to arrive at the y value.
| X Value | Equation | Y value |
| y = −6x + 2 | ||
| 1 | y = −6(1) + 2 | -4 |
| 2 | y = −6(2) + 2 | -10 |
| 3 | y = −6(3) + 2 | -16 |
| 4 | y = −6(4) + 2 | -22 |
An Optional step, if you want, you can omit the middle column from your table, since the table of values is really just the x and y pairs .(We used the middle column simply to help us get the y values)
| X Value | Y value |
| 1 | -4 |
| 2 | -10 |
| 3 | -16 |
| 4 | -22 |
Problem 3
Create a table of values of the equation y = −6x − 4
Create the table and choose a set of x values
| X Value | Equation | Y value |
| y = −6x − 4 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Substitute each x value (left side column) into the equation.
| X Value | Equation | Y value |
| 1 | y = −6(1) − 4 | |
| 2 | y = −6(2) − 4 | |
| 3 | y = −6(3) − 4 | |
| 4 | y = −6(4) − 4 |
Evaluate the equation (middle column) to arrive at the y value.
| X Value | Equation | Y value |
| 1 | y = −6(1) − 4 | -10 |
| 2 | y = −6(2) − 4 | -16 |
| 3 | y = −6(3) − 4 | -22 |
| 4 | y = −6(4) − 4 | -28 |
An Optional step, if you want, you can omit the middle column from your table, since the table of values is really just the x and y pairs. (We used the middle column simply to help us get the y values)
| X Value | Y value |
| 1 | -10 |
| 2 | -16 |
| 3 | -22 |
| 4 | -28 |

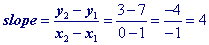
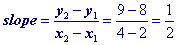
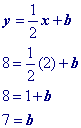
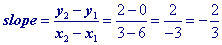
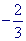 x + b
x + b